You Are What You Eat – AI Alignment Requires Understanding How Data Shapes Structure and Generalisation

Authors

Simon Pepin Lehalleur ⁼

University of Amsterdam

Jesse Hoogland ⁼

Timaeus

Matthew Farrugia-Roberts ⁼

University of Oxford

Susan Wei

Monash University

Alexander Gietelink Oldenziel

Timaeus & University College London

George Wang

Timaeus

Stan van Wingerden

Timaeus

Zach Furman

University of Melbourne

Liam Carroll

Timaeus & Gradient Institute

Daniel Murfet

University of Melbourne

See Contributions

Publication Details

Published:

February 8, 2025

Access

Abstract

In this position paper, we argue that understanding the relation between structure in the data distribution and structure in trained models is central to AI alignment. First, we discuss how two neural networks can have equivalent performance on the training set but compute their outputs in essentially different ways and thus generalise differently. For this reason, standard testing and evaluation are insufficient for obtaining assurances of safety for widely deployed generally intelligent systems. We argue that to progress beyond evaluation to a robust mathematical science of AI alignment, we need to develop statistical foundations for an understanding of the relation between structure in the data distribution, internal structure in models, and how these structures underlie generalisation.

Automated Conversion Notice

Warning: This paper was automatically converted from LaTeX. While we strive for accuracy, some formatting or mathematical expressions may not render perfectly. Please refer to the original ArXiv version for the authoritative document.

1 Introduction

The alignment problem was stated by the mathematician Wiener (1960) as follows: “If we use, to achieve our purposes, a mechanical agency with whose operation we cannot interfere effectively… we had better be quite sure that the purpose put into the machine is the purpose which we really desire.” What is it that we are putting into our machines, and how sure are we that it is instilling in them our desired purposes? In the era of large-scale deep learning, AI alignment techniques rely on shaping the training data distribution. In turn, this data distribution shapes the internal structures that develop inside the model. These internal structures determine the model’s behaviour, including its alignment properties. In this paper, we argue for the position that achieving a deep scientific understanding of this pipeline – from data, to internal structure, through to generalisation – is necessary for AI alignment.

The paper is organised as follows:

In Section 2, we outline what is known about how internal structure in neural networks emerges over training, how this structure is shaped by patterns in the data distribution, and how this structure plays a role in determining the model’s generalisation behaviour.
In Section 3, we describe the alignment problem¹¹1This paper does not debate the importance of AI alignment or safety; it presumes the reader recognises these as critical issues. Instead, we focus on the need for new theoretical paradigms to address core challenges in AI alignment. and we argue that most modern alignment techniques function by shaping the training data distribution (thus, indirectly shaping structure and generalisation).
In Section 4, we review what we understand about how data shapes structure in learning systems. We recall the theory of internal model selection in Bayesian inference with singular model classes, which predicts that in some cases, a simpler, less accurate model can be preferred over an accurate but more complex model.
In Section 5, we argue that in the context of attempting to align powerful AI models to a complex system of human values, this kind of inductive bias can cause a problem since many data distributions may lead to simplistic and dangerous alternative solutions.
In Section 6, we defend our position: If you want to solve the alignment problem by shaping the data distribution, you need a deep understanding of how data shapes structure and how structure determines generalisation. We sketch several research avenues that would contribute towards this goal.

We conclude by considering two alternative views (Section 7): a structural understanding of generalisation may be unnecessary for alignment, and may be intractable. We nevertheless argue that, as during the advent of previous powerful and dangerous technologies, we should not expect to get away safely with only a shallow, empirical understanding of how AI systems develop. Moreover, while the project we outline is sure to be a challenging enterprise, this does not mean it is not necessary.

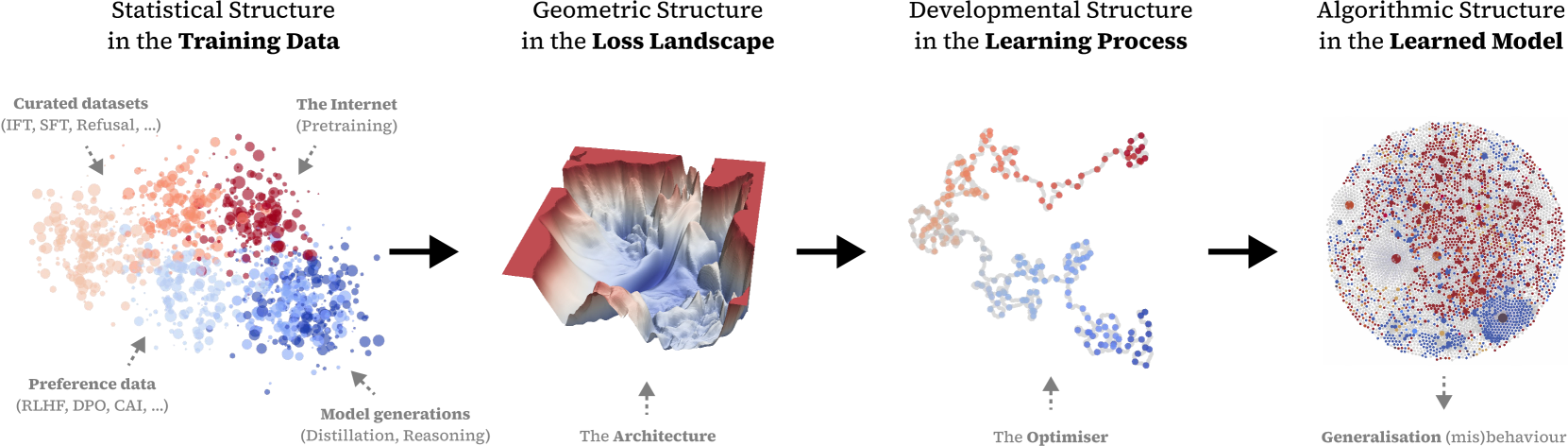
Refer to caption — Figure 1: **From data to model behaviour**: Structure in data determines internal structure in models and thus generalisation. Current approaches to alignment work by shaping the training distribution (left), which only indirectly determines model structure (right) through the effects on shaping the optimisation process (middle left & right). To mitigate the limitations of this indirect approach, alignment requires a better understanding of these intermediate links (loss visualisation from Li et al. 2018; “S4 correspondence” based on Wang et al. 2024).

2 Patterns, Structures, and Generalisation

In this section, we outline how neural networks display emergent internal structure, how this structure is shaped by patterns in the data distribution, and the relation to generalisation. This process is summarised in Figure 1, which describes the flow of structure from the training data through the geometry of the loss landscape and the unfolding of the training process into the internal structure of the model (building on the “S4 correspondence” of Wang et al. 2024).

2.1 Internal Structure in Models

“Understanding data and understanding models that work on that data are intimately linked. In fact, I think that understanding your model has to imply understanding the data it works on.”

— Chris Olah, Visualizing Representations, 2015

In classical statistics, parametrised statistical models are small, and the structure they possess is the structure that we give them (e.g., in a graphical model). In the modern era of machine learning, models are large and initially unorganised and progressively acquire “structure” throughout training (Nanda et al., 2023; Wang et al., 2024; Tigges et al., 2024).

Research in mechanistic interpretability has begun to uncover interesting internal algorithmic structure in neural networks, such as “circuits” for various tasks (Olah et al., 2020; Cammarata et al., 2020; Sharkey et al., 2025). Researchers have identified circuits for indirect object identification (Wang et al., 2022), activation patterns corresponding to individuals, emotions, and programming concepts (Templeton et al., 2024), and even structures that seem to implement mathematical operations (Nanda et al., 2023). These findings suggest that models develop internal representations and algorithms that go beyond simple pattern matching or memorisation. That is not to say that we expect algorithms in neural networks to be as “clean” as traditional programs; we expect these learned programs to often behave like ensembles of partial programs and heuristics. While we’ve made progress in identifying these learned algorithms, the connection between this internal structure and generalisation remains to be mathematically clarified (Olsson et al., 2022; He et al., 2024).

From a fundamental point of view, it is not surprising that neural networks acquire algorithmic structure: modern deep learning systems achieve low loss on their training objectives by effectively compressing the data distribution (Shwartz-Ziv & Tishby, 2017; Delétang et al., 2023), and a useful form of compression is learning to represent the underlying generative process (Schmidhuber, 1992; Bengio et al., 2012; Ha & Schmidhuber, 2018). Learning as compression is also the key idea of the minimum description length principle (MDL), which is equivalent in some regimes to Bayesian inference (Grünwald & Roos, 2020).

2.2 Structure in the World

The concept of structure in the world as a precondition for learning has deep roots in philosophy and science (Plato, c. 360 BCE; Bacon, 1620). Classical statistics (e.g., Cox 2006) formalises this notion through the idea of a “true” model – a specific probability distribution believed to have generated the observed dataset. In this paradigm, learning involves using the data to accurately estimate the parameters of this true probability distribution. With the true model, prediction is a straightforward, subsidiary task.

However, the reliance on a true model in inferential statistics has faced long-standing criticism (Rissanen, 1989; Breiman, 2001; Cox, 2006). The advent of modern deep learning has intensified this scrutiny (Sejnowski, 2020). In deep learning, a model’s predictive performance is valued over its veracity.

Given deep learning’s empirical success, we are compelled to re-examine what it means to learn parameters from data – in this case, neural network weights from training data. Notably, no one believes that a CNN trained on CIFAR is learning the precise underlying probability distribution of the images. Furthermore, due to a lack of identifiability, multiple neural network weight configurations can yield the same loss – and thus the same likelihood – although they may not perform equivalently in other respects. This raises a critical question: If there is no single true parameter and many parameters result in equivalent loss, what exactly are we learning when we optimise neural network weights?

We posit that the success of deep learning in modelling complex phenomena suggests a form of structure in the world that is algorithmic in nature. In this perspective, algorithms themselves can be viewed as latent features of the world. This view aligns with classic work on inductive inference in algorithmic information theory (Solomonoff, 1964) as well as more recent work in computational mechanics (Crutchfield, 2012), which propose that the most concise description of a process is often algorithmic and that the simpler algorithms realising a given process are more likely.

This is consistent with decades of research in cognitive neuroscience. For example, Rogers & McClelland (2004) argue that a natural explanation for internal structure in biological and artificial neural networks is that it mirrors internal structure in the data. Further, they argue for a relationship between these two kinds of structure and structure in the learning process, such as developmental stages. Recent work in deep learning (Saxe et al., 2018; Hoogland et al., 2024; Wang et al., 2024) has provided evidence supporting the applicability of this view to artificial neural networks.

The emergence of coherent computational structures across different scales (Lieberum et al., 2023) further support the idea that these learned algorithms may reflect intrinsic properties of the world rather than artefacts of specific models (Huh et al., 2024), although see Chughtai et al. (2023). In the alignment discourse, a related point of view has been articulated by Wentworth; see Chan et al. (2023). This viewpoint not only offers a lens for understanding deep learning but also calls for a re-evaluation of classical statistics in light of these algorithmic forms of structure implicit in data.

2.3 Underspecification and Generalisation

“However, in singular learning machines, the role of the parameter is not uniquely determined, hence even by checking the parameter, we cannot examine whether the model’s learning is subject to the designer’s intention.”

— Sumio Watanabe, 2024, §3.4

The modern era of deep learning is characterised by a focus on scaling up model size, dataset size, and training compute as the principal engine of capability improvement. The belief in this approach, often referred to as the “scaling hypothesis,” was articulated and popularised by Branwen (2020) based on earlier observations (Sutton, 2019; Amodei & Hernandez, 2018; Raffel et al., 2019). The scaling hypothesis suggests that many AI capabilities might emerge primarily as a consequence of increasing scale rather than through fundamental algorithmic breakthroughs. This idea gained empirical support through work on scaling laws (Hestness et al., 2017; Kaplan et al., 2020) and the success of GPT-3 (Brown et al., 2020; Bommasani et al., 2021).

In this paradigm, AI development resembles industrial chemical synthesis. Just as chemical engineers carefully control reactants, catalysts, and conditions to yield desired products, as predicted by reaction kinetics, AI engineers manipulate training data distributions, model architectures, and optimisation processes to produce models with targeted test losses, as predicted by scaling laws. However, unlike industrial chemical synthesis, the exact properties and capabilities of the resulting systems are not known in advance.

One reason for this uncertainty, beyond our poor understanding of SGD dynamics, is underspecification (D’Amour et al., 2022), where the training distribution does not specify a unique solution. There can be a large set of low-loss parameters that all satisfy the constraints enforced by the loss function equally well (Yang et al., 2021; Reizinger et al., 2024; Papyan, 2019; Hochreiter & Schmidhuber, 1997; Fort & Ganguli, 2019; Chen et al., 2023a). Among these low-loss parameters, there may be solutions that solve the problem in qualitatively different ways or, in other words, that generalise differently outside of the training distribution.

It is our position that these differences in generalisation arise from differences in internal algorithms and representations. Thus, if we care about what happens when the model is deployed in new contexts, then we must study the structure that the model has learned and not merely its performance on the training set or evaluations (Watanabe, 2024, §3.4). We ideally want AI training to qualify as an engineering process, where we have sufficient control over the behaviour of the final product in its intended environment, even if this differs from the training environment.

3 AI Alignment by Data Distribution Shaping

In this section, we describe what we mean by alignment and then review state-of-the-art methods for AI alignment, most of which function by shaping the data distribution so as to indirectly program model behaviour.

3.1 The Alignment Problem

While concerns about alignment have existed since the beginning of computer science (Turing, 1948; Good, 1966), the discourse gained momentum in the early 21st century (Yudkowsky, 2004; Bostrom, 2014). Recent progress in artificial intelligence has brought a new focus to AI misalignment as a source of profound risks (Russell, 2019; Bengio et al., 2023; Anwar et al., 2024). We refer the reader to Everitt et al. (2018); Christiano (2019); Ngo (2020) for background on the alignment problem.

For our purposes, it suffices to define AI alignment as the problem of ensuring an AI system is trying to do what a human wants it to do. This formulation is sometimes referred to as intent alignment. We note that we do not consider the broader, but not less important question of whose purposes should guide the machine (Christiano 2018, Ngo 2020, §4).

We also note that AI alignment is a subfield of the broader field of AI safety and that we expect that the perspective put forth here will prove useful for other questions in AI safety, as the problem of generalisation runs through the whole subject (Kosoy, 2018; Sharkey et al., 2025; Burns et al., 2023; Ilyas et al., 2019; Casper et al., 2023; Korbak et al., 2025; Anwar et al., 2024).

3.2 AI Alignment Techniques

Many current approaches to AI alignment attempt to shape model behaviour indirectly by curating the “ingredients” of the learning process. One common approach is fine-tuning a pretrained model on a carefully selected dataset that embodies the desired behaviours or knowledge. Instruction tuning, a specific form of fine-tuning, focuses on datasets composed of task instructions paired with desired outputs, aiming to make models more adept at following human instructions (Wei et al., 2021). Another prominent technique is Reinforcement Learning from Human Feedback (RLHF), which uses human preferences to guide the model towards desired behaviours (Ouyang et al., 2022). Other state-of-the-art approaches include Constitutional AI (Bai et al., 2022b), Direct Preference Optimisation (DPO; Rafailov et al. 2023), and Deliberative Alignment (Guan et al., 2024). These methods all fundamentally operate by modifying the effective data distribution the model experiences during training. These alignment methods aim to alter the loss landscape, guiding the optimisation process towards parameter configurations that encode desired behaviours.

4 So, How Does Data Shape Structure?

In this section, we review what we do understand about how data shapes structure in learning systems. Prior work on this topic points to a principle by which patterns in the data distribution are represented by computational structure in models, and, moreover, “deeper” patterns are represented by correspondingly “deeper” structures.

As a precise example, we recall results from the field of singular learning theory that describe a principle of internal model selection in Bayesian inference, whereby in some cases a simpler, less accurate model can be preferred over an accurate but more complex model (Watanabe, 2009, §7.6).

4.1 Deep vs. Shallow Structure

The structure present in training data is not uniformly significant; some patterns may explain a greater proportion of the variability in the data and, consequently, may be more deeply encoded into the learned models. The idea of a hierarchy of distributional structure leading to a hierarchy of structures within learning systems has been emphasised in representation learning (Bengio et al., 2012) and explored in the context of developmental neuroscience (Johnson & de Haan, 2015; Kiebel & Friston, 2011) and in the literature on artificial neural networks (Achille et al., 2018; Abbe et al., 2023).

This phenomenon has been demonstrated concretely in several settings. For example, Saxe et al. (2018) demonstrate that in deep linear networks, modes of the input-output covariance matrix with higher singular values are learned earlier and more robustly. Similarly, Canatar et al. (2020) show that in both kernel regression and infinitely wide neural networks, functions aligned with the principal components of the data covariance matrix corresponding to larger eigenvalues are learned faster and generalise better. Empirical studies of small transformer language models validate this hierarchical learning pattern, showing a progression from simple bigram patterns through n-grams to more complex structures like induction and nested parenthesis matching (Hoogland et al., 2024; Wang et al., 2024). These findings provide a grounding for the intuition that some structures in the data are indeed “deeper” than others in the sense that they are more readily and stably learned by neural networks.

4.2 Singular Learning Theory

For over two decades Sumio Watanabe has developed a mathematical framework for understanding the nature of generalisation in a class of learning systems that includes neural networks. This framework is called singular learning theory (SLT; Watanabe, 2009, 2018, see Wei et al., 2023; Watanabe, 2022 for an overview).

To date, most of the results in SLT apply in the setting of Bayesian inference, whereby instead of training a neural network by SGD, one studies the evolution of the Bayesian posterior distribution with increasing numbers of samples. In practice, the parameters that are found by SGD are not necessarily those that are the most probable according to the posterior. Nonetheless, recent empirical work that has applied the ideas of SLT to the setting of deep learning has found it a useful guide towards an understanding of the principles governing the development of internal structure (Chen et al., 2023b; Hoogland et al., 2024; Wang et al., 2024; Urdshals & Nasufi, 2024; Carroll et al., 2025).

4.3 Internal Model Selection

For the purposes of our discussion, it suffices to outline the principle of internal model selection in Bayesian inference as studied in SLT Watanabe, 2009, §7.6; Chen et al., 2023b; see also Carroll et al., 2025.

Consider a neural network parameter space $\mathcal{W}\subseteq\mathbb{R}^{d}$ . Let $\varphi(w)$ be a nonzero prior (which, by analogy with practical deep learning initialisations, may be taken to be an independent Gaussian for each weight) and $\ell_{n}:\mathcal{W}\to\mathbb{R}$ an empirical loss (the average negative log-likelihood) on $n$ samples. Then the Bayesian posterior probability of a region $\mathcal{U}\subseteq\mathcal{W}$ given $n$ samples is

p_{n}(\mathcal{U})=\frac{Z_{n}(\mathcal{U})}{Z_{n}(\mathcal{W})},

where $Z_{n}(\mathcal{X})$ , for $\mathcal{X}\subseteq\mathcal{W}$ , is given by

Z_{n}(\mathcal{X})=\int_{\mathcal{X}}\exp(-n\ell_{n}(w))\varphi(w)\,dw.

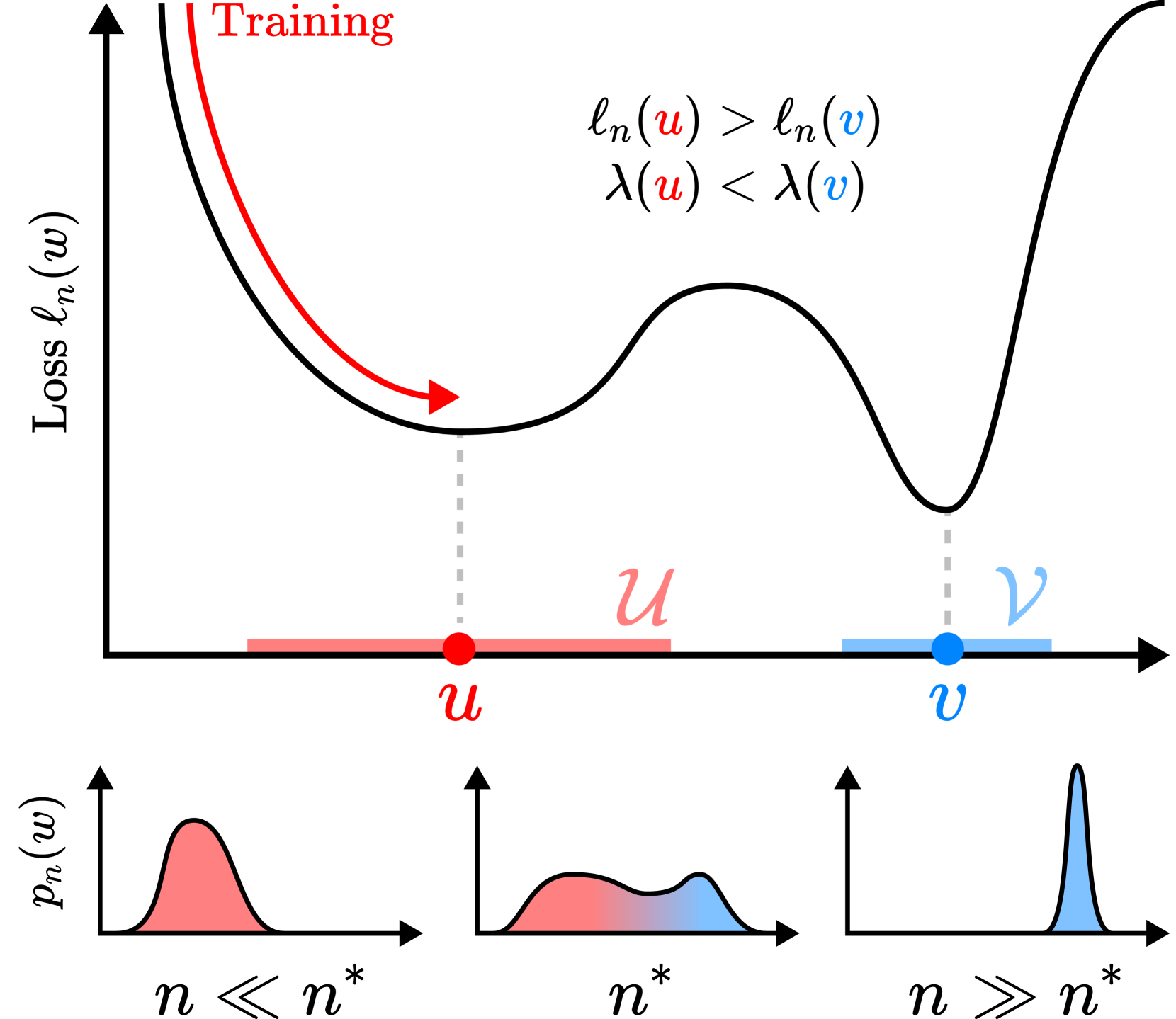
Consider a case in which two neighbourhoods, $\mathcal{U},\mathcal{V}\subseteq\mathcal{W}$ , each contain a local minimum of the population loss, which we think of respectively as a simple but misaligned solution and a complex but aligned solution. The preference of the Bayesian posterior for $\mathcal{U}$ over $\mathcal{V}$ can be summarised in the posterior log-odds,

\log\frac{p_{n}(\mathcal{U})}{p_{n}(\mathcal{V})}=\log Z_{n}(\mathcal{U})-\log Z% _{n}(\mathcal{V}),

(1)

which is positive to the extent that the posterior distribution prefers $\mathcal{U}$ over $\mathcal{V}$ .

SLT can help us to understand this situation. Let $u\in\mathcal{W}$ be a local minimum of the expected negative log-likelihood, and let $\mathcal{U}$ be a closed ball around $u$ , in which $u$ is a maximally degenerate global minimum. Then, under certain technical conditions, we have the following asymptotic expansion in $n$ Watanabe, 2018, Theorem 11; Lau et al., 2025:

-\log Z_{n}(\mathcal{U})=\ell_{n}(u)\cdot n+\lambda(u)\cdot\log n+O_{p}(\log% \log n)

(2)

where $\lambda(u)$ is the local learning coefficient (LLC; Lau et al. 2025) a measure of model complexity which is represented in Figure 2 by basin flatness (simpler solutions, with broader basins, have a lower local learning coefficient). The local learning coefficient can be estimated from data via a refinement of Equation 2, but it depends on the data-generating distribution and measures “how efficiently” the model with parameters $u$ is approximating it.

If $v\in\mathcal{V}$ is a competing solution (with its own neighbourhood), then Equation 1 and Equation 2 give

\log\frac{p_{n}(\mathcal{U})}{p_{n}(\mathcal{V})}=\Delta\ell_{n}\cdot n+\Delta% \lambda\cdot\log n+O_{p}(\log\log n)

(3)

where $\Delta\ell_{n}=\ell_{n}(v)-\ell_{n}(u)$ and $\Delta\lambda=\lambda(v)-\lambda(u)$ .

Assume the lower-order terms from each expansion cancel. Then if $\Delta\ell_{n}<0$ ( $u$ has higher loss than $v$ ) and $\Delta\lambda>0$ ( $u$ has lower LLC than $v$ ), the sign of the log-odds depends on $n$ . The function $n/\log(n)$ is increasing and the Bayesian posterior will prefer $\mathcal{U}$ (around the simple but inaccurate solution) as long as $n/\log(n)<\Delta\lambda/(-\Delta\ell_{n})$ , after which it will prefer $\mathcal{V}$ (around the accurate but complex solution).

Thus for $n$ sufficiently large we will get what we asked for, in the sense that the region $\mathcal{V}$ dominates the posterior; this is the solution that we were attempting to specify with the training data. However for finite $n$ we may obtain a simplification of our intent in the sense that $\mathcal{U}$ dominates.

Recent work by Carroll et al. (2025) has used the above logic to study transformers trained for in-context linear regression. In that example there is a region $\mathcal{U}$ containing a generalising solution and a region $\mathcal{V}$ containing a memorising solution. They find that SGD trajectories first approach the generalising solution (with lower estimated LLC) before converging to the memorising solution (with higher estimated LLC). That is, the SGD trajectories behave with increasing steps $t$ in a way similar to the Bayesian posterior with increasing $n$ . This suggests that, despite the differences between SGD and Bayesian inference, the phenomena described above does occur in deep learning.

5 Inductive Biases Against Alignment

In this section, we argue that in the context of attempting to align powerful AI models to a complex system of human values, the kind of inductive biases discussed in Section 4 can lead to misalignment, since many data distributions may contain “deep patterns” representing simplistic and/or dangerous alternative solutions, even if the data distribution uniquely specifies perfectly aligned behaviour at optimality.

5.1 Shortcuts and the Complexity of Alignment

Implementing the values specified in the training data may require accurate representations of many contingent rules, edge cases, and subtle moral distinctions (Yudkowsky, 2007). By contrast, it can be significantly simpler (in the sense of using fewer effective parameters) for a model to learn a heuristic strategy that complies with the specification on most training inputs but fails to truly internalise the intended objective.

Suppose we conceptualise alignment as the provision of a constitution and thousands of pages of specifications, which together “point” to a coherent and unique mode of behaviour. That is, the aligned behaviour is the unique global minimum of the associated population loss. It is reasonable to expect that among those complex specifications there are opportunities for “shortcuts” which lead to simpler but less well-aligned behaviours. As discussed in Section 4.3, SLT provides a proof-of-concept suggesting that training could find, and perhaps remain, at these undesirable interpretations of the training data. In practice, compression techniques like pruning or quantisation, used to deploy models on edge devices like phones or robots, will tend to sacrifice performance in order to lower complexity (Cheng et al., 2018; Choudhary et al., 2020), exacerbating the above problem.

The complexity of human values and the relation between misalignment, Occam’s razor, and inductive biases of SGD have been widely discussed in the alignment literature (Yudkowsky, 2007; Christiano, 2016; Hubinger, 2019; Hubinger et al., 2019; Cohen et al., 2024). Hubinger et al. (2024) discuss deceptive instrumental alignment in terms similar to those in Section 4.3. They point out that many generalisations are consistent with the training data and that inductive biases of pretraining and safety fine-tuning are important for judging the likelihood of deceptive alignment (Hubinger et al., 2024, §2.1).

5.2 Deep and Dangerous Patterns in Real World Data

As AI systems become more advanced and more integrated into society, their training data is likely to include many fundamental patterns that are present in the natural world, some of which we do not want to be represented in their behaviour.

One version of this concern, due to Omohundro (2018) and Bostrom (2014), is “instrumental convergence,” where certain sub-goals or behaviours are likely to emerge across a wide range of terminal goals due to their broad utility, potentially leading to their robust encoding in trained models (see also Ngo, 2020). From the perspective of this paper, instrumental convergence is both a claim about what rational agents would want, as well as an empirically anchored hypothesis about which data patterns are consistently discovered and reinforced by large neural models.

Another example is the “Queen’s dilemma” (Murfet, 2024): as a result of internalising the pattern that human decision-making is comparatively incompetent, a superhuman AI might sideline human input without ever openly contradicting it. This highlights a subtle alignment failure: as AI systems recognise and adapt to our relative limitations, they may effectively strip away meaningful human oversight while preserving the formal appearance of it.

5.3 Distribution Shift

Techniques like supervised fine-tuning and RLHF are surprisingly effective at shaping next-token predictors into assistants (Bai et al., 2022a; Ouyang et al., 2022). This shows the power of engineering the data distribution as a technique for aligning AI systems.

However, our understanding of how these techniques actually modify the internal representations and algorithms of the models remains limited (Anwar et al., 2024; Barez et al., 2025). Moreover, there are concerns about the depth and stability of the changes induced by these alignment techniques. Research has shown that safety fine-tuning as it is currently performed can be easily undone (Gade et al., 2023; Qi et al., 2023). This suggests that current methods do not result in deep, stable alterations to the model’s core functionality; rather they create shallow, easily disrupted structures.

When there is a significant change in the data distribution, such as the shift from training to deployment, the structures associated with alignment might be more fragile than those associated with core capabilities This leads to the concerning possibility that “capabilities generalize further than alignment” (Soares, 2023). Distribution shift is a well-studied topic in machine learning and in the AI alignment discourse (Amodei et al., 2016, §7), but our theoretical and empirical understanding of the comparative robustness of different kinds of structures to different kinds of changes in the data distribution remains limited.

6 Understanding is Necessary

In this section, we bring together our arguments and defend our position – that understanding the relationship between data, internal structure, and generalisation is crucial for alignment. We outline promising directions for future work towards this goal and the further challenge of aligning future agentic AI systems, which play a role in their own data-generating process.

6.1 Why We Need Understanding

There is a general consensus that we do not yet know how to align general human-level or superintelligent AI systems, that our alignment of current AI systems is not robust, and that an important component of progress in alignment is understanding AI systems better (Bengio et al., 2025; Anwar et al., 2024).

We have made the case that algorithmic structure in models determines their behaviour, that this structure is shaped by structure in the data distribution, and that current alignment techniques aim to indirectly program model behaviour by carefully designing the data distribution.

Since we do not understand the chain of influence from changes in data to changes in behaviour, alignment is an inexact science, and we have no current basis for confidence in our ability to align advanced AI systems. In particular, we argued that the flexibility of this indirect form of programming leads to a unique set of risks, including deceptive alignment, instrumental convergence, and vulnerability to distribution shift.

6.2 Promising Future Directions

We see two broad areas where fundamental progress will be required in order to achieve a sufficient understanding of the relations between data, structure and generalisation, and where non-trivial progress seems possible in the short term:

Interpretability (learning to read): we should work towards mathematical foundations for mechanistic interpretability in Bayesian statistics as well as other mathematical, statistical and physical frameworks, thereby linking our best empirical tools for inferring internal structure to rigorous theories of generalisation.
Patterning (learning to write): our current practices for shaping model behaviour in post-training should develop towards a science of “pattern engineering” where we understand the patterns we are putting into the data and how they affect the resulting behaviour of models. That is, we should aim to gradually move from indirect to direct programming of model behaviour.

6.3 A Further Challenge: Reinforcement Learning

As demonstrated by recent reasoning models like OpenAI’s o1, reinforcement learning (RL) will be a key component of training the next generations of AI models, far beyond its current role in post-training techniques like RLHF (OpenAI et al., 2024; DeepSeek-AI et al., 2025). Future alignment techniques will need to work not just for LLMs but also for agents.

For that reason, any foundational approaches to understanding the link between data, structure and generalisation must account for the fact that in reinforcement learning (RL), the data distribution not only shapes the model, but is also shaped by the model through the actions that the agent takes. RL poses a number of other challenges for alignment: e.g., less human-interpretable representations, jumps to superhuman performance, and goal misgeneralisation (Langosco et al., 2022; Cohen et al., 2024). Tackling these problems requires building on work in non i.i.d. Bayesian statistics (Su & Mukherjee, 2021; Adams & Mukherjee, 2024) and connections between RL and Bayesian inference (Levine, 2018).

7 Alternative Views

We now present some alternative perspectives that challenge our position that understanding the connection between data, structure, and generalisation is central to alignment.

7.1 Empiricism is Enough

One counterargument is that theoretical understanding may be unnecessary for alignment. Perhaps the empirical alignment approaches championed to date (Askell et al., 2021; Bai et al., 2022b; Ouyang et al., 2022) will continue to be sufficient to align future generations of AI models. After all, we have required essentially no theoretical understanding of the link between structure and generalisation to advance machine learning to its present-day capabilities (Sutton, 2019).

However, history shows that when technological systems are pushed to operate far outside their normal conditions, theoretical understanding often becomes critical for ensuring safety and control.

The Industrial Revolution provides an instructive parallel: it began with practical engineering and “tinkering” rather than theoretical understanding (Cardwell, 1971; Mokyr, 1992). But as steam engines were pushed to operate at increasingly extreme pressures and temperatures, accidents and fatalities occurred, which prompted government safety investigations in Britain and France. A deeper theoretical understanding of thermodynamics became necessary to ensure safety (Cardwell, 1971, pp.177–180).

As our technological capabilities have advanced, pushing the world into more and more extreme states, this pattern has repeated – from steam engines to internal combustion engines to nuclear reactors. Modern nuclear power plants, while building on empirical insights, could not operate safely without deep theoretical foundations in nuclear physics and thermodynamics (Zohuri & McDaniel, 2015). As more advanced AI systems are deployed, they may also push the world to conditions far out of the training distribution, amplifying the risks associated with misgeneralisation and thereby increasing the need for theoretical progress.

7.2 Understanding is Intractable

Another criticism is that deeply understanding the relationship between data, structure, and generalisation may be fundamentally intractable (Hendrycks, 2025; Yampolskiy, 2020). From this view, alignment efforts would be better directed toward deployment guardrails and policy interventions rather than a deeper understanding of how structure emerges in these systems (e.g., Greenblatt et al. 2024).

Recent developments in mechanistic interpretability have challenged the extreme version of this view: simple techniques like Sparse Autoencoders (SAEs) have discovered rich, interpretable structure in large language models (Templeton et al., 2024). If anything, larger models could be more interpretable: the increased capacity may enable models to converge on simpler, shared “Platonic” structure (Huh et al., 2024) as in double descent (Nakkiran et al., 2021; Belkin et al., 2020).

The fundamental question, then, is not whether interpretability is possible – these advances have established that it is – but rather to what degree it is achievable. Unfortunately, it is quite plausible that the degree of understanding needed for safety may be intractable. Yet the history of science offers many examples where seemingly impenetrable barriers ultimately fall; we recall Eddington’s prescient words on the “impossible” task of understanding the insides of stars:

At first sight it would seem that the deep interior of the sun and stars is less accessible to scientific investigation than any other region of the universe. Our telescopes may probe farther and farther into the depths of space; but how can we ever obtain certain knowledge of that which is hidden behind substantial barriers? […] We do not, however, study the interior of a star merely out of curiosity as to the extraordinary conditions prevailing there. It appears that an understanding of the mechanism of the interior throws light on the external manifestations of the star, and the whole theory is ultimately brought into contact with observation. At least that is the goal which we keep in view.

— Arthur Eddington, 1926

8 Conclusion

As AI systems become more powerful, their behaviour outside the training distribution becomes more consequential. The core challenge of alignment is ensuring that these systems maintain desired behaviours even as they operate in novel contexts. This fundamentally depends on how learned behaviours generalise – and generalisation is grounded in internal computational structures shaped by the data distribution. Understanding this connection between data, structure, and generalisation is therefore central to alignment.

Progress in alignment of superintelligent systems may ultimately depend on our ability to transition from viewing AI development as a form of alchemy – where we shape behaviour through empirical trial and error with data distributions – to a true engineering discipline grounded in a deep understanding of how structure propagates from data to models. A scientific and rigorous approach grounded in singular learning theory, interpretability research, and careful empirical study may offer our best hope for embedding robust, stable alignment at the core of powerful AI systems.

Acknowledgements. SPL is supported by the European Research Council (ERC), grant 864145.

References

Abbe et al. (2023) Abbe, E., Adsera, E. B., and Misiakiewicz, T. SGD learning on neural networks: leap complexity and saddle-to-saddle dynamics. In The Thirty Sixth Annual Conference on Learning Theory, pp. 2552–2623. PMLR, 2023.
Achille et al. (2018) Achille, A., Rovere, M., and Soatto, S. Critical learning periods in deep networks. In International Conference on Learning Representations, September 2018. URL https://openreview.net/forum?id=BkeStsCcKQ.
Adams & Mukherjee (2024) Adams, Z. P. and Mukherjee, S. Meta-posterior consistency for the bayesian inference of metastable system, August 2024. Preprint arXiv:2408.01868 [stat.ML].
Amodei & Hernandez (2018) Amodei, D. and Hernandez, D. AI and compute. OpenAI Blog, May 2018. URL https://openai.com/index/ai-and-compute/.
Amodei et al. (2016) Amodei, D., Olah, C., Steinhardt, J., Christiano, P., Schulman, J., and Mané, D. Concrete problems in AI safety, June 2016. Preprint arXiv:1606.06565 [cs.AI].
Anwar et al. (2024) Anwar, U., Saparov, A., Rando, J., Paleka, D., Turpin, M., Hase, P., Lubana, E. S., Jenner, E., Casper, S., Sourbut, O., Edelman, B. L., Zhang, Z., Günther, M., Korinek, A., Hernandez-Orallo, J., Hammond, L., Bigelow, E. J., Pan, A., Langosco, L., Korbak, T., Zhang, H. C., Zhong, R., hÉigeartaigh, S. O., Recchia, G., Corsi, G., Chan, A., Anderljung, M., Edwards, L., Petrov, A., de Witt, C. S., Motwani, S. R., Bengio, Y., Chen, D., Torr, P., Albanie, S., Maharaj, T., Foerster, J. N., Tramèr, F., He, H., Kasirzadeh, A., Choi, Y., and Krueger, D. Foundational challenges in assuring alignment and safety of large language models. Transactions on Machine Learning Research, 2024. ISSN 2835-8856. Survey Certification, Expert Certification.
Askell et al. (2021) Askell, A., Bai, Y., Chen, A., Drain, D., Ganguli, D., Henighan, T., Jones, A., Joseph, N., Mann, B., DasSarma, N., et al. A general language assistant as a laboratory for alignment, 2021.
Bacon (1620) Bacon, F. Novum Organum. In Latin. Translated into English by Fowler (1878).
Bai et al. (2022a) Bai, Y., Jones, A., Ndousse, K., Askell, A., Chen, A., DasSarma, N., Drain, D., Fort, S., Ganguli, D., Henighan, T., Joseph, N., Kadavath, S., Kernion, J., Conerly, T., El-Showk, S., Elhage, N., Hatfield-Dodds, Z., Hernandez, D., Hume, T., Johnston, S., Kravec, S., Lovitt, L., Nanda, N., Olsson, C., Amodei, D., Brown, T., Clark, J., McCandlish, S., Olah, C., Mann, B., and Kaplan, J. Training a helpful and harmless assistant with reinforcement learning from human feedback, April 2022a. Preprint arXiv:2204.05862 [cs.CL].
Bai et al. (2022b) Bai, Y., Kadavath, S., Kundu, S., Askell, A., Kernion, J., Jones, A., Chen, A., Goldie, A., Mirhoseini, A., McKinnon, C., Chen, C., Olsson, C., Olah, C., Hernandez, D., Drain, D., Ganguli, D., Li, D., Tran-Johnson, E., Perez, E., Kerr, J., Mueller, J., Ladish, J., Landau, J., Ndousse, K., Lukosuite, K., Lovitt, L., Sellitto, M., Elhage, N., Schiefer, N., Mercado, N., DasSarma, N., Lasenby, R., Larson, R., Ringer, S., Johnston, S., Kravec, S., Showk, S. E., Fort, S., Lanham, T., Telleen-Lawton, T., Conerly, T., Henighan, T., Hume, T., Bowman, S. R., Hatfield-Dodds, Z., Mann, B., Amodei, D., Joseph, N., McCandlish, S., Brown, T., and Kaplan, J. Constitutional AI: Harmlessness from ai feedback, December 2022b. Preprint arXiv:2212.08073 [cs.CL].
Barez et al. (2025) Barez, F., Fu, T., Prabhu, A., Casper, S., Sanyal, A., Bibi, A., O’Gara, A., Kirk, R., Bucknall, B., Fist, T., Ong, L., Torr, P., Lam, K.-Y., Trager, R., Krueger, D., Mindermann, S., Hernandez-Orallo, J., Geva, M., and Gal, Y. Open problems in machine unlearning for AI safety, January 2025. Preprint arXiv:2501.04952 [cs.LG].
Belkin et al. (2020) Belkin, M., Hsu, D., and Xu, J. Two models of double descent for weak features. SIAM Journal on Mathematics of Data Science, 2(4):1167–1180, 2020.
Bengio et al. (2012) Bengio, Y., Courville, A., and Vincent, P. Representation learning: A review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(8):1798–1828, June 2012. doi: 10.1109/TPAMI.2013.50.
Bengio et al. (2023) Bengio, Y., Hinton, G., Yao, A., Song, D., Abbeel, P., Darrell, T., Harari, Y. N., Zhang, Y.-Q., Xue, L., Shalev-Shwartz, S., Hadfield, G., Clune, J., Maharaj, T., Hutter, F., Baydin, A. G., McIlraith, S., Gao, Q., Acharya, A., Krueger, D., Dragan, A., Torr, P., Russell, S., Kahneman, D., Brauner, J., and Mindermann, S. Managing extreme AI risks amid rapid progress, October 2023. Preprint arXiv:2310.17688 [cs.CY].
Bengio et al. (2025) Bengio, Y., Mindermann, S., Privitera, D., Besiroglu, T., Bommasani, R., Casper, S., Choi, Y., Fox, P., Garfinkel, B., Goldfarb, D., Heidari, H., Ho, A., Kapoor, S., Khalatbari, L., Longpre, S., Manning, S., Mavroudis, V., Mazeika, M., Michael, J., Newman, J., Ng, K. Y., Okolo, C. T., Raji, D., Sastry, G., Seger, E., Skeadas, T., South, T., Strubell, E., Tramèr, F., Velasco, L., Wheeler, N., Acemoglu, D., Adekanmbi, O., Dalrymple, D., Dietterich, T. G., Felten, E. W., Fung, P., Gourinchas, P.-O., Heintz, F., Hinton, G., Jennings, N., Krause, A., Leavy, S., Liang, P., Ludermir, T., Marda, V., Margetts, H., McDermid, J., Munga, J., Narayanan, A., Nelson, A., Neppel, C., Oh, A., Ramchurn, G., Russell, S., Schaake, M., Schölkopf, B., Song, D., Soto, A., Tiedrich, L., Varoquaux, G., Yao, A., Zhang, Y.-Q., Ajala, O., Albalawi, F., Alserkal, M., Avrin, G., Busch, C., de Carvalho, A. C. P. d. L. F., Fox, B., Gill, A. S., Hatip, A. H., Heikkilä, J., Johnson, C., Jolly, G., Katzir, Z., Khan, S. M., Kitano, H., Krüger, A., Lee, K. M., Ligot, D. V., López Portillo, J. R., Molchanovskyi, O., Monti, A., Mwamanzi, N., Nemer, M., Oliver, N., Pezoa Rivera, R., Ravindran, B., Riza, H., Rugege, C., Seoighe, C., Sheehan, J., Sheikh, H., Wong, D., and Zeng, Y. International AI safety report: The international scientific report on the safety of advanced AI. Technical Report DSIT 2025/001, AI Action Summit, January 2025. URL https://www.gov.uk/government/publications/international-ai-safety-report-2025.
Bommasani et al. (2021) Bommasani, R., Hudson, D. A., Adeli, E., Altman, R., Arora, S., Arx, S. v., Bernstein, M. S., Bohg, J., Bosselut, A., Brunskill, E., Brynjolfsson, E., Buch, S., Card, D., Castellon, R., Chatterji, N., Chen, A., Creel, K., Davis, J. Q., Demszky, D., Donahue, C., Doumbouya, M., Durmus, E., Ermon, S., Etchemendy, J., Ethayarajh, K., Fei-Fei, L., Finn, C., Gale, T., Gillespie, L., Goel, K., Goodman, N., Grossman, S., Guha, N., Hashimoto, T., Henderson, P., Hewitt, J., Ho, D. E., Hong, J., Hsu, K., Huang, J., Icard, T., Jain, S., Jurafsky, D., Kalluri, P., Karamcheti, S., Keeling, G., Khani, F., Khattab, O., Koh, P. W., Krass, M., Krishna, R., Kuditipudi, R., Kumar, A., Ladhak, F., Lee, M., Lee, T., Leskovec, J., Levent, I., Li, X. L., Li, X., Ma, T., Malik, A., Manning, C. D., Mirchandani, S., Mitchell, E., Munyikwa, Z., Nair, S., Narayan, A., Narayanan, D., Newman, B., Nie, A., Niebles, J. C., Nilforoshan, H., Nyarko, J., Ogut, G., Orr, L., Papadimitriou, I., Park, J. S., Piech, C., Portelance, E., Potts, C., Raghunathan, A., Reich, R., Ren, H., Rong, F., Roohani, Y., Ruiz, C., Ryan, J., Ré, C., Sadigh, D., Sagawa, S., Santhanam, K., Shih, A., Srinivasan, K., Tamkin, A., Taori, R., Thomas, A. W., Tramèr, F., Wang, R. E., Wang, W., Wu, B., Wu, J., Wu, Y., Xie, S. M., Yasunaga, M., You, J., Zaharia, M., Zhang, M., Zhang, T., Zhang, X., Zhang, Y., Zheng, L., Zhou, K., and Liang, P. On the opportunities and risks of foundation models, August 2021. Preprint arXiv:2108.07258 [cs.LG].
Bostrom (2014) Bostrom, N. Superintelligence: Paths, Dangers, Strategies. Oxford University Press, 2014.
Branwen (2020) Branwen, G. The scaling hypothesis, 2020. URL https://www.gwern.net/Scaling-Hypothesis. Accessed: 2023-08-05.
Breiman (2001) Breiman, L. Statistical modeling: The two cultures (with comments and a rejoinder by the author). Statistical Science, 16(3):199–231, 2001.
Brown et al. (2020) Brown, T., Mann, B., Ryder, N., Subbiah, M., Kaplan, J. D., Dhariwal, P., Neelakantan, A., Shyam, P., Sastry, G., Askell, A., et al. Language models are few-shot learners. Advances in Neural Information Processing Systems, 33:1877–1901, 2020.
Burns et al. (2023) Burns, C., Izmailov, P., Kirchner, J. H., Baker, B., Gao, L., Aschenbrenner, L., Chen, Y., Ecoffet, A., Joglekar, M., Leike, J., et al. Weak-to-strong generalization: Eliciting strong capabilities with weak supervision. In International Conference on Machine Learning, 2023.
Bury (1929) Bury, R. G. Timaeus. Critias. Cleitophon. Menexenus. Epistles, chapter 1, pp. 1–254. Number 234 in Loeb Classical Library. Harvard University Press, 1929. English translation of Plato (c. 360 BCE).
Cammarata et al. (2020) Cammarata, N., Olah, C., Schubert, L., Goh, G., Petrov, M., and Carter, S. Thread: Circuits. Distill, March 2020. doi: 10.23915/distill.00024. https://distill.pub/2020/circuits.
Canatar et al. (2020) Canatar, A., Bordelon, B., and Pehlevan, C. Spectral bias and task-model alignment explain generalization in kernel regression and infinitely wide neural networks. Nature Communications, 12(1):2914, June 2020. doi: 10.1038/s41467-021-23103-1.
Cardwell (1971) Cardwell, D. S. L. From Watt to Clausius: The Rise of Thermodynamics in the Early Industrial Age. Cornell University Press, 1971.
Carroll et al. (2025) Carroll, L., Hoogland, J., Farrugia-Roberts, M., and Murfet, D. Dynamics of transient structure in in-context linear regression transformers, January 2025. Preprint arXiv:2501.17745 [cs.LG].
Casper et al. (2023) Casper, S., Davies, X., Shi, C., Gilbert, T. K., Scheurer, J., Rando, J., Freedman, R., Korbak, T., Lindner, D., Freire, P., Wang, T. T., Marks, S., Segerie, C.-R., Carroll, M., Peng, A., Christoffersen, P. J., Damani, M., Slocum, S., Anwar, U., Siththaranjan, A., Nadeau, M., Michaud, E. J., Pfau, J., Krasheninnikov, D., Chen, X., Langosco, L., Hase, P., Biyik, E., Dragan, A., Krueger, D., Sadigh, D., and Hadfield-Menell, D. Open problems and fundamental limitations of reinforcement learning from human feedback. Transactions on Machine Learning Research, September 2023. ISSN 2835-8856. URL https://openreview.net/forum?id=bx24KpJ4Eb. Survey Certification, Featured Certification.
Chan et al. (2023) Chan, L., Lang, L., and Jenner, E. Natural abstractions: Key claims, theorems, and critiques. LessWrong, 2023. URL https://www.lesswrong.com/posts/gvzW46Z3BsaZsLc25.
Chen et al. (2023a) Chen, F., Kunin, D., Yamamura, A., and Ganguli, S. Stochastic collapse: How gradient noise attracts SGD dynamics towards simpler subnetworks. Neural Information Processing Systems, 2023a.
Chen et al. (2023b) Chen, Z., Lau, E., Mendel, J., Wei, S., and Murfet, D. Dynamical versus bayesian phase transitions in a toy model of superposition, October 2023b. Preprint arXiv:2310.06301 [cs.LG].
Cheng et al. (2018) Cheng, Y., Wang, D., Zhou, P., and Zhang, T. Model compression and acceleration for deep neural networks: The principles, progress, and challenges. IEEE Signal Processing Magazine, 35(1):126–136, 2018. doi: 10.1109/MSP.2017.2765695.
Choudhary et al. (2020) Choudhary, T., Mishra, V., Goswami, A., and Sarangapani, J. A comprehensive survey on model compression and acceleration. Artificial Intelligence Review, 53(7):5113–5155, 2020. doi: 10.1007/s10462-020-09816-7.
Christiano (2016) Christiano, P. What does the universal prior actually look like? Ordinary Ideas (Blog), 2016. URL https://ordinaryideas.wordpress.com/2016/11/30/what-does-the-universal-prior-actually-look-like/.
Christiano (2018) Christiano, P. Clarifying AI alignment. LessWrong, 2018. URL https://www.lesswrong.org/posts/ZeE7EKHTFMBs8eMxn.
Christiano (2019) Christiano, P. What failure looks like. LessWrong, 2019. URL https://www.lesswrong.com/posts/HBxe6wdjxK239zajf.
Chughtai et al. (2023) Chughtai, B., Chan, L., and Nanda, N. A toy model of universality: Reverse engineering how networks learn group operations. In International Conference on Machine Learning, 2023.
Cohen et al. (2024) Cohen, M. K., Hutter, M., Bengio, Y., and Russell, S. RL, but don’t do anything I wouldn’t do, 2024. Preprint arXiv:2410.06213 [cs.LG].
Copeland (2004) Copeland, B. J. (ed.). The Essential Turing: Seminal Writings in Computing, Logic, Philosophy, Artificial Intelligence, and Artificial Life: Plus The Secrets of Enigma, chapter 10, pp. 404–432. Oxford University Press, 2004. Restoration and republication of Turing (1948), with introduction.
Cox (2006) Cox, D. R. Principles of Statistical Inference. Cambridge University Press, 2006.
Crutchfield (2012) Crutchfield, J. P. Between order and chaos. Nature Physics, 8(1):17–24, 2012.
D’Amour et al. (2022) D’Amour, A., Heller, K., Moldovan, D., Adlam, B., Alipanahi, B., Beutel, A., Chen, C., Deaton, J., Eisenstein, J., Hoffman, M. D., et al. Underspecification presents challenges for credibility in modern machine learning. Journal of Machine Learning Research, 23(226):1–61, 2022.
DeepSeek-AI et al. (2025) DeepSeek-AI, Guo, D., Yang, D., Zhang, H., Song, J., Zhang, R., Xu, R., Zhu, Q., Ma, S., Wang, P., Bi, X., Zhang, X., Yu, X., Wu, Y., Wu, Z. F., Gou, Z., Shao, Z., Li, Z., Gao, Z., Liu, A., Xue, B., Wang, B., Wu, B., Feng, B., Lu, C., Zhao, C., Deng, C., Zhang, C., Ruan, C., Dai, D., Chen, D., Ji, D., Li, E., Lin, F., Dai, F., Luo, F., Hao, G., Chen, G., Li, G., Zhang, H., Bao, H., Xu, H., Wang, H., Ding, H., Xin, H., Gao, H., Qu, H., Li, H., Guo, J., Li, J., Wang, J., Chen, J., Yuan, J., Qiu, J., Li, J., Cai, J. L., Ni, J., Liang, J., Chen, J., Dong, K., Hu, K., Gao, K., Guan, K., Huang, K., Yu, K., Wang, L., Zhang, L., Zhao, L., Wang, L., Zhang, L., Xu, L., Xia, L., Zhang, M., Zhang, M., Tang, M., Li, M., Wang, M., Li, M., Tian, N., Huang, P., Zhang, P., Wang, Q., Chen, Q., Du, Q., Ge, R., Zhang, R., Pan, R., Wang, R., Chen, R. J., Jin, R. L., Chen, R., Lu, S., Zhou, S., Chen, S., Ye, S., Wang, S., Yu, S., Zhou, S., Pan, S., Li, S. S., Zhou, S., Wu, S., Ye, S., Yun, T., Pei, T., Sun, T., Wang, T., Zeng, W., Zhao, W., Liu, W., Liang, W., Gao, W., Yu, W., Zhang, W., Xiao, W. L., An, W., Liu, X., Wang, X., Chen, X., Nie, X., Cheng, X., Liu, X., Xie, X., Liu, X., Yang, X., Li, X., Su, X., Lin, X., Li, X. Q., Jin, X., Shen, X., Chen, X., Sun, X., Wang, X., Song, X., Zhou, X., Wang, X., Shan, X., Li, Y. K., Wang, Y. Q., Wei, Y. X., Zhang, Y., Xu, Y., Li, Y., Zhao, Y., Sun, Y., Wang, Y., Yu, Y., Zhang, Y., Shi, Y., Xiong, Y., He, Y., Piao, Y., Wang, Y., Tan, Y., Ma, Y., Liu, Y., Guo, Y., Ou, Y., Wang, Y., Gong, Y., Zou, Y., He, Y., Xiong, Y., Luo, Y., You, Y., Liu, Y., Zhou, Y., Zhu, Y. X., Xu, Y., Huang, Y., Li, Y., Zheng, Y., Zhu, Y., Ma, Y., Tang, Y., Zha, Y., Yan, Y., Ren, Z. Z., Ren, Z., Sha, Z., Fu, Z., Xu, Z., Xie, Z., Zhang, Z., Hao, Z., Ma, Z., Yan, Z., Wu, Z., Gu, Z., Zhu, Z., Liu, Z., Li, Z., Xie, Z., Song, Z., Pan, Z., Huang, Z., Xu, Z., Zhang, Z., and Zhang, Z. DeepSeek-R1: Incentivizing reasoning capability in LLMs via reinforcement learning, January 2025. Preprint arXiv:2501.12948 [cs.CL].
Delétang et al. (2023) Delétang, G., Ruoss, A., Duquenne, P.-A., Catt, E., Genewein, T., Mattern, C., Grau-Moya, J., Wenliang, L. K., Aitchison, M., Orseau, L., Hutter, M., and Veness, J. Language modeling is compression. In International Conference on Learning Representations, 2023.
Eddington (1926) Eddington, A. S. The Internal Constitution of the Stars. Cambridge University Press, 1926. Reissued in the Cambridge Science Classics series, 1988.
Everitt et al. (2018) Everitt, T., Lea, G., and Hutter, M. AGI safety literature review. In International Joint Conference on Artificial Intelligence, pp. 5441–5449. International Joint Conferences on Artificial Intelligence Organization, July 2018. doi: 10.24963/ijcai.2018/768.
Fort & Ganguli (2019) Fort, S. and Ganguli, S. Emergent properties of the local geometry of neural loss landscapes, October 2019. Preprint arXiv:1910.05929 [cs.LG].
Fowler (1878) Fowler, T. Bacon’s Novum Organum. Clarendon Press, 1878. Annotated English translation of Bacon (1620).
Gade et al. (2023) Gade, P., Lermen, S., Rogers-Smith, C., and Ladish, J. BadLlama: cheaply removing safety fine-tuning from Llama 2-Chat 13B, October 2023. Preprint arXiv:2311.00117 [cs.CL].
Good (1966) Good, I. J. Speculations concerning the first ultraintelligent machine. Advances in Computers, pp. 31–88, 1966. doi: 10.1016/S0065-2458(08)60418-0.
Greenblatt et al. (2024) Greenblatt, R., Shlegeris, B., Sachan, K., and Roger, F. AI control: Improving safety despite intentional subversion. In Forty-First International Conference on Machine Learning, June 2024.
Grünwald & Roos (2020) Grünwald, P. and Roos, T. Minimum description length revisited. International Journal of Mathematics for Industry, 11(01):1930001, March 2020. doi: 10.1142/S2661335219300018.
Guan et al. (2024) Guan, M. Y., Joglekar, M., Wallace, E., Jain, S., Barak, B., Helyar, A., Dias, R., Vallone, A., Ren, H., Wei, J., Chung, H. W., Toyer, S., Heidecke, J., Beutel, A., and Glaese, A. Deliberative alignment: Reasoning enables safer language models, December 2024. Preprint arXiv:2412.16339 [cs.CL].
Ha & Schmidhuber (2018) Ha, D. and Schmidhuber, J. World models, March 2018. Preprint arxiv:1803.10122 [cs].
He et al. (2024) He, T., Doshi, D., Das, A., and Gromov, A. Learning to grok: Emergence of in-context learning and skill composition in modular arithmetic tasks. In The Thirty-eighth Annual Conference on Neural Information Processing Systems, June 2024.
Hendrycks (2025) Hendrycks, D. Introduction to AI Safety, Ethics, and Society. Taylor & Francis, 2025.
Hestness et al. (2017) Hestness, J., Narang, S., Ardalani, N., Diamos, G., Jun, H., Kianinejad, H., Patwary, M. M. A., Yang, Y., and Zhou, Y. Deep learning scaling is predictable, empirically, December 2017.
Hochreiter & Schmidhuber (1997) Hochreiter, S. and Schmidhuber, J. Flat minima. Neural Computation, 9(1):1–42, 1997.
Hoogland et al. (2024) Hoogland, J., Wang, G., Farrugia-Roberts, M., Carroll, L., Wei, S., and Murfet, D. The developmental landscape of in-context learning, February 2024. Preprint arXiv:2402.02364 [cs.LG].
Hubinger (2019) Hubinger, E. Are minimal circuits deceptive? LessWrong, 2019. URL https://www.lesswrong.com/posts/fM5ZWGDbnjb7ThNKJ.
Hubinger et al. (2019) Hubinger, E., Merwijk, C. v., Mikulik, V., Skalse, J., and Garrabrant, S. Risks from learned optimization in advanced machine learning systems, June 2019. Preprint arXiv:1906.01820 [cs.AI].
Hubinger et al. (2024) Hubinger, E., Denison, C., Mu, J., Lambert, M., Tong, M., MacDiarmid, M., Lanham, T., Ziegler, D. M., Maxwell, T., Cheng, N., Jermyn, A., Askell, A., Radhakrishnan, A., Anil, C., Duvenaud, D., Ganguli, D., Barez, F., Clark, J., Ndousse, K., Sachan, K., Sellitto, M., Sharma, M., DasSarma, N., Grosse, R., Kravec, S., Bai, Y., Witten, Z., Favaro, M., Brauner, J., Karnofsky, H., Christiano, P., Bowman, S. R., Graham, L., Kaplan, J., Mindermann, S., Greenblatt, R., Shlegeris, B., Schiefer, N., and Perez, E. Sleeper agents: Training deceptive LLMs that persist through safety training, January 2024. Preprint arXiv:2401.05566 [cs.CR].
Huh et al. (2024) Huh, M., Cheung, B., Wang, T., and Isola, P. The platonic representation hypothesis. In International Conference on Machine Learning, 2024.
Ilyas et al. (2019) Ilyas, A., Santurkar, S., Tsipras, D., Engstrom, L., Tran, B., and Madry, A. Adversarial examples are not bugs, they are features. Advances in neural information processing systems, 32, 2019.
Johnson & de Haan (2015) Johnson, M. H. and de Haan, M. D. Developmental Cognitive Neuroscience: An Introduction. John Wiley & Sons, June 2015.
Kaplan et al. (2020) Kaplan, J., McCandlish, S., Henighan, T., Brown, T. B., Chess, B., Child, R., Gray, S., Radford, A., Wu, J., and Amodei, D. Scaling laws for neural language models, January 2020. Preprint arXiv:2001.08361 [cs.LG].
Kiebel & Friston (2011) Kiebel, S. J. and Friston, K. J. Free energy and dendritic self-organization. Frontiers in Systems Neuroscience, 5, July 2011. doi: 10.3389/fnsys.2011.00080.
Korbak et al. (2025) Korbak, T., Clymer, J., Hilton, B., Shlegeris, B., and Irving, G. A sketch of an AI control safety case, January 2025. Preprint arXiv:2501.17315 [cs.AI].
Kosoy (2018) Kosoy, V. The learning theoretic alignment agenda. LessWrong, 2018. URL https://www.lesswrong.com/posts/5bd75cc58225bf0670375575.
Langosco et al. (2022) Langosco, L., Koch, J., Sharkey, L. D., Pfau, J., and Krueger, D. Goal misgeneralization in deep reinforcement learning. In International Conference on Machine Learning, pp. 12004–12019. PMLR, 2022.
Lau et al. (2025) Lau, E., Furman, Z., Wang, G., Murfet, D., and Wei, S. The local learning coefficient: A singularity-aware complexity measure. In The 28th International Conference on Artificial Intelligence and Statistics, 2025. URL https://openreview.net/forum?id=1av51ZlsuL. To appear. Preprint arXiv:2308.12108 [stat.ML].
Levine (2018) Levine, S. Reinforcement learning and control as probabilistic inference: Tutorial and review, May 2018. Preprint arXiv:1805.00909 [cs.LG].
Li et al. (2018) Li, H., Xu, Z., Taylor, G., Studer, C., and Goldstein, T. Visualizing the loss landscape of neural nets. Advances in Neural Information Processing Systems, 31, 2018.
Lieberum et al. (2023) Lieberum, T., Rahtz, M., Kramár, J., Nanda, N., Irving, G., Shah, R., and Mikulik, V. Does circuit analysis interpretability scale? evidence from multiple choice capabilities in chinchilla, July 2023. Preprint arXiv:2307.09458 [cs.LG].
Mokyr (1992) Mokyr, J. The Lever of Riches: Technological Creativity and Economic Progress. Oxford University Press, 1992.
Murfet (2024) Murfet, D. The queen’s dilemma: A paradox of control. LessWrong, 2024. URL https://www.lesswrong.com/posts/ui3AztyGKCpHA5ZhM.
Nakkiran et al. (2021) Nakkiran, P., Kaplun, G., Bansal, Y., Yang, T., Barak, B., and Sutskever, I. Deep double descent: Where bigger models and more data hurt. Journal of Statistical Mechanics: Theory and Experiment, 2021(12):124003, 2021.
Nanda et al. (2023) Nanda, N., Chan, L., Lieberum, T., Smith, J., and Steinhardt, J. Progress measures for grokking via mechanistic interpretability. In International Conference on Learning Representations, 2023.
Ngo (2020) Ngo, R. AGI safety from first principles. Alignment Forum, 2020. URL https://www.alignmentforum.org/s/mzgtmmTKKn5MuCzFJ.
Olah (2015) Olah, C. Visualizing representations: Deep learning and human beings, January 2015. URL https://colah.github.io/posts/2015-01-Visualizing-Representations/.
Olah et al. (2020) Olah, C., Cammarata, N., Schubert, L., Goh, G., Petrov, M., and Carter, S. Zoom in: An introduction to circuits. Distill, 5, March 2020. doi: 10.23915/distill.00024.001. https://distill.pub/2020/circuits/zoom-in.
Olsson et al. (2022) Olsson, C., Elhage, N., Nanda, N., Joseph, N., DasSarma, N., Henighan, T., Mann, B., Askell, A., Bai, Y., Chen, A., Conerly, T., Drain, D., Ganguli, D., Hatfield-Dodds, Z., Hernandez, D., Johnston, S., Jones, A., Kernion, J., Lovitt, L., Ndousse, K., Amodei, D., Brown, T., Clark, J., Kaplan, J., McCandlish, S., and Olah, C. In-context learning and induction heads. Transformer Circuits Thread, 2022.
Omohundro (2018) Omohundro, S. M. The basic AI drives. In Artificial Intelligence Safety and Security, pp. 47–55. Chapman and Hall/CRC, July 2018. doi: 10.1201/9781351251389-3.
OpenAI et al. (2024) OpenAI, :, Jaech, A., Kalai, A., Lerer, A., Richardson, A., El-Kishky, A., Low, A., Helyar, A., Madry, A., Beutel, A., Carney, A., Iftimie, A., Karpenko, A., Passos, A. T., Neitz, A., Prokofiev, A., Wei, A., Tam, A., Bennett, A., Kumar, A., Saraiva, A., Vallone, A., Duberstein, A., Kondrich, A., Mishchenko, A., Applebaum, A., Jiang, A., Nair, A., Zoph, B., Ghorbani, B., Rossen, B., Sokolowsky, B., Barak, B., McGrew, B., Minaiev, B., Hao, B., Baker, B., Houghton, B., McKinzie, B., Eastman, B., Lugaresi, C., Bassin, C., Hudson, C., Li, C. M., Bourcy, C. d., Voss, C., Shen, C., Zhang, C., Koch, C., Orsinger, C., Hesse, C., Fischer, C., Chan, C., Roberts, D., Kappler, D., Levy, D., Selsam, D., Dohan, D., Farhi, D., Mely, D., Robinson, D., Tsipras, D., Li, D., Oprica, D., Freeman, E., Zhang, E., Wong, E., Proehl, E., Cheung, E., Mitchell, E., Wallace, E., Ritter, E., Mays, E., Wang, F., Such, F. P., Raso, F., Leoni, F., Tsimpourlas, F., Song, F., Lohmann, F. v., Sulit, F., Salmon, G., Parascandolo, G., Chabot, G., Zhao, G., Brockman, G., Leclerc, G., Salman, H., Bao, H., Sheng, H., Andrin, H., Bagherinezhad, H., Ren, H., Lightman, H., Chung, H. W., Kivlichan, I., O’Connell, I., Osband, I., Gilaberte, I. C., Akkaya, I., Kostrikov, I., Sutskever, I., Kofman, I., Pachocki, J., Lennon, J., Wei, J., Harb, J., Twore, J., Feng, J., Yu, J., Weng, J., Tang, J., Yu, J., Candela, J. Q., Palermo, J., Parish, J., Heidecke, J., Hallman, J., Rizzo, J., Gordon, J., Uesato, J., Ward, J., Huizinga, J., Wang, J., Chen, K., Xiao, K., Singhal, K., Nguyen, K., Cobbe, K., Shi, K., Wood, K., Rimbach, K., Gu-Lemberg, K., Liu, K., Lu, K., Stone, K., Yu, K., Ahmad, L., Yang, L., Liu, L., Maksin, L., Ho, L., Fedus, L., Weng, L., Li, L., McCallum, L., Held, L., Kuhn, L., Kondraciuk, L., Kaiser, L., Metz, L., Boyd, M., Trebacz, M., Joglekar, M., Chen, M., Tintor, M., Meyer, M., Jones, M., Kaufer, M., Schwarzer, M., Shah, M., Yatbaz, M., Guan, M. Y., Xu, M., Yan, M., Glaese, M., Chen, M., Lampe, M., Malek, M., Wang, M., Fradin, M., McClay, M., Pavlov, M., Wang, M., Wang, M., Murati, M., Bavarian, M., Rohaninejad, M., McAleese, N., Chowdhury, N., Chowdhury, N., Ryder, N., Tezak, N., Brown, N., Nachum, O., Boiko, O., Murk, O., Watkins, O., Chao, P., Ashbourne, P., Izmailov, P., Zhokhov, P., Dias, R., Arora, R., Lin, R., Lopes, R. G., Gaon, R., Miyara, R., Leike, R., Hwang, R., Garg, R., Brown, R., James, R., Shu, R., Cheu, R., Greene, R., Jain, S., Altman, S., Toizer, S., Toyer, S., Miserendino, S., Agarwal, S., Hernandez, S., Baker, S., McKinney, S., Yan, S., Zhao, S., Hu, S., Santurkar, S., Chaudhuri, S. R., Zhang, S., Fu, S., Papay, S., Lin, S., Balaji, S., Sanjeev, S., Sidor, S., Broda, T., Clark, A., Wang, T., Gordon, T., Sanders, T., Patwardhan, T., Sottiaux, T., Degry, T., Dimson, T., Zheng, T., Garipov, T., Stasi, T., Bansal, T., Creech, T., Peterson, T., Eloundou, T., Qi, V., Kosaraju, V., Monaco, V., Pong, V., Fomenko, V., Zheng, W., Zhou, W., McCabe, W., Zaremba, W., Dubois, Y., Lu, Y., Chen, Y., Cha, Y., Bai, Y., He, Y., Zhang, Y., Wang, Y., Shao, Z., and Li, Z. OpenAI o1 system card, December 2024. Preprint arXiv:2412.16720 [cs.AI].
Ouyang et al. (2022) Ouyang, L., Wu, J., Jiang, X., Almeida, D., Wainwright, C. L., Mishkin, P., Zhang, C., Agarwal, S., Slama, K., Ray, A., Schulman, J., Hilton, J., Kelton, F., Miller, L., Simens, M., Askell, A., Welinder, P., Christiano, P., Leike, J., and Lowe, R. Training language models to follow instructions with human feedback. Neural Information Processing Systems, 2022.
Papyan (2019) Papyan, V. Measurements of three-level hierarchical structure in the outliers in the spectrum of deepnet hessians. In International Conference on Machine Learning, pp. 5012–5021. PMLR, January 2019.
Plato (c. 360 BCE) Plato. Timaeus. c. 360 BCE. In Ancient Greek. Translated into English by Bury (1929).
Qi et al. (2023) Qi, X., Zeng, Y., Xie, T., Chen, P.-Y., Jia, R., Mittal, P., and Henderson, P. Fine-tuning aligned language models compromises safety, even when users do not intend to! In The Twelfth International Conference on Learning Representations, October 2023.
Rafailov et al. (2023) Rafailov, R., Sharma, A., Mitchell, E., Manning, C. D., Ermon, S., and Finn, C. Direct preference optimization: Your language model is secretly a reward model. Neural Information Processing Systems, 2023.
Raffel et al. (2019) Raffel, C., Shazeer, N., Roberts, A., Lee, K., Narang, S., Matena, M., Zhou, Y., Li, W., and Liu, P. J. Exploring the limits of transfer learning with a unified text-to-text transformer. Journal of Machine Learning Research, 21(140):1–67, October 2019.
Reizinger et al. (2024) Reizinger, P., Ujváry, S., Mészáros, A., Kerekes, A., Brendel, W., and Huszár, F. Position: Understanding LLMs requires more than statistical generalization. In Proceedings of the 41st International Conference on Machine Learning, volume 235 of Proceedings of Machine Learning Research, pp. 42365–42390. PMLR, 21–27 Jul 2024.
Rissanen (1989) Rissanen, J. Stochastic Complexity in Statistical Inquiry, volume 15. World Scientific, November 1989. doi: 10.1142/0822.
Rogers & McClelland (2004) Rogers, T. T. and McClelland, J. L. Semantic Cognition. MIT Press, June 2004. doi: 10.7551/mitpress/6161.001.0001.
Russell (2019) Russell, S. Human Compatible: Artificial Intelligence and the Problem of Control. Penguin, October 2019.
Saxe et al. (2018) Saxe, A. M., McClelland, J. L., and Ganguli, S. A mathematical theory of semantic development in deep neural networks. Proceedings of the National Academy of Sciences, 116(23):11537 – 11546, October 2018. doi: 10.1073/pnas.1820226116.
Schmidhuber (1992) Schmidhuber, J. Learning complex, extended sequences using the principle of history compression. Neural Computation, 4(2):234–242, 1992.
Sejnowski (2020) Sejnowski, T. J. The unreasonable effectiveness of deep learning in artificial intelligence. Proceedings of the National Academy of Sciences, 117(48):30033–30038, December 2020. ISSN 0027-8424, 1091-6490. doi: 10.1073/pnas.1907373117.
Sharkey et al. (2025) Sharkey, L., Chughtai, B., Batson, J., Lindsey, J., Wu, J., Bushnaq, L., Goldowsky-Dill, N., Heimersheim, S., Ortega, A., Bloom, J., Biderman, S., Garriga-Alonso, A., Conmy, A., Nanda, N., Rumbelow, J., Wattenberg, M., Schoots, N., Miller, J., Michaud, E. J., Casper, S., Tegmark, M., Saunders, W., Bau, D., Todd, E., Geiger, A., Geva, M., Hoogland, J., Murfet, D., and McGrath, T. Open problems in mechanistic interpretability, January 2025. Preprint arXiv:2501.16496 [cs.LG].
Shwartz-Ziv & Tishby (2017) Shwartz-Ziv, R. and Tishby, N. Opening the black box of deep neural networks via information, March 2017. Preprint arXiv:1703.00810 [cs.LG].
Soares (2023) Soares, N. Deep deceptiveness. LessWrong, 2023. URL https://www.lesswrong.org/posts/XWwvwytieLtEWaFJX.
Solomonoff (1964) Solomonoff, R. J. A formal theory of inductive inference. Part I. Information and Control, 7(1):1–22, 1964. doi: 10.1016/s0019-9958(64)90223-2.
Su & Mukherjee (2021) Su, L. and Mukherjee, S. Large deviation asymptotics and bayesian posterior consistency on stochastic processes and dynamical systems, June 2021. Preprint arXiv:2106.06894 [math.ST].
Sutton (2019) Sutton, R. The bitter lesson, March 2019. URL http://incompleteideas.net/IncIdeas/BitterLesson.html. Incomplete Ideas (Blog).
Templeton et al. (2024) Templeton, A., Conerly, T., Marcus, J., Lindsey, J., Bricken, T., Chen, B., Pearce, A., Citro, C., Ameisen, E., Jones, A., Cunningham, H., Turner, N. L., McDougall, C., MacDiarmid, M., Freeman, C. D., Sumers, T. R., Rees, E., Batson, J., Jermyn, A., Carter, S., Olah, C., and Henighan, T. Scaling monosemanticity: Extracting interpretable features from Claude 3 Sonnet. Transformer Circuits Thread, 2024. URL https://transformer-circuits.pub/2024/scaling-monosemanticity/index.html.
Tigges et al. (2024) Tigges, C., Hanna, M., Yu, Q., and Biderman, S. LLM circuit analyses are consistent across training and scale. In The Thirty-eighth Annual Conference on Neural Information Processing Systems, November 2024.
Turing (1948) Turing, A. Intelligent machinery. Technical report, National Physical Laboratory, 1948. Restored and republished by Copeland (2004).
Urdshals & Nasufi (2024) Urdshals, E. and Nasufi, J. Structure Development in List Sorting Transformers. In NeurIPS 2024 Workshop on Scientific Methods for Understanding Deep Learning, November 2024.
Wang et al. (2024) Wang, G., Hoogland, J., Van Wingerden, S., Furman, Z., and Murfet, D. Differentiation and Specialization of Attention Heads via the Refined Local Learning Coefficient. In The Thirteenth International Conference on Learning Representations, October 2024.
Wang et al. (2022) Wang, K., Variengien, A., Conmy, A., Shlegeris, B., and Steinhardt, J. Interpretability in the wild: a circuit for indirect object identification in GPT-2 small, November 2022. Preprint arXiv:2211.00593 [cs.LG].
Watanabe (2009) Watanabe, S. Algebraic Geometry and Statistical Learning Theory. Cambridge University Press, 2009.
Watanabe (2018) Watanabe, S. Mathematical Theory of Bayesian Statistics. CRC Press, Taylor & Francis Group, USA, April 2018. doi: 10.1201/9781315373010.
Watanabe (2022) Watanabe, S. Recent advances in algebraic geometry and Bayesian statistics. Information Geometry, 7(Suppl 1):187–209, November 2022. doi: 10.48550/arXiv.2211.10049.
Watanabe (2024) Watanabe, S. Review and prospect of algebraic research in equivalent framework between statistical mechanics and machine learning theory, May 2024. Preprint arXiv:2406.10234 [cond-mat.stat-mech].
Wei et al. (2021) Wei, J., Bosma, M., Zhao, V. Y., Guu, K., Yu, A. W., Lester, B., Du, N., Dai, A. M., and Le, Q. V. Finetuned language models are zero-shot learners. In International Conference on Learning Representations, 2021.
Wei et al. (2023) Wei, S., Murfet, D., Gong, M., Li, H., Gell-Redman, J., and Quella, T. Deep learning is singular, and that’s good. IEEE Transactions on Neural Networks and Learning Systems, 34(12):10473–10486, December 2023. doi: 10.1109/TNNLS.2022.3167409.
Wiener (1960) Wiener, N. Some moral and technical consequences of automation. Science, 131(3410):1355–1358, 1960.
Yampolskiy (2020) Yampolskiy, R. V. Unexplainability and incomprehensibility of AI. Journal of Artificial Intelligence and Consciousness, 7(02):277–291, 2020.
Yang et al. (2021) Yang, R., Mao, J., and Chaudhari, P. Does the data induce capacity control in deep learning? In Proceedings of the 39th International Conference on Machine Learning, volume abs/2110.14163 of Proceedings of Machine Learning Research, pp. 25166–25197. PMLR, October 2021.
Yudkowsky (2004) Yudkowsky, E. Coherent extrapolated volition. Technical report, Singularity Institute for Artificial Intelligence, 2004. URL https://intelligence.org/files/CEV.pdf.
Yudkowsky (2007) Yudkowsky, E. The hidden complexity of wishes. LessWrong, 2007. URL https://www.lesswrong.com/posts/4ARaTpNX62uaL86j6.
Zohuri & McDaniel (2015) Zohuri, B. and McDaniel, P. Thermodynamics in Nuclear Power Plant Systems. Springer, 2015.

Cite as

@article{lehalleur2025you,
  title = {You Are What You Eat – AI Alignment Requires Understanding How Data Shapes Structure and Generalisation},
  author = {Simon Pepin Lehalleur and Jesse Hoogland and Matthew Farrugia-Roberts and Susan Wei and Alexander Gietelink Oldenziel and George Wang and Stan van Wingerden and Zach Furman and Liam Carroll and Daniel Murfet},
  year = {2025},
  abstract = {In this position paper, we argue that understanding the relation between structure in the data distribution and structure in trained models is central to AI alignment. First, we discuss how two neural networks can have equivalent performance on the training set but compute their outputs in essentially different ways and thus generalise differently. For this reason, standard testing and evaluation are insufficient for obtaining assurances of safety for widely deployed generally intelligent systems. We argue that to progress beyond evaluation to a robust mathematical science of AI alignment, we need to develop statistical foundations for an understanding of the relation between structure in the data distribution, internal structure in models, and how these structures underlie generalisation.},
  eprint = {2502.05475},
  archivePrefix = {arXiv},
  url = {https://arxiv.org/abs/2502.05475}
}

Click to copy