We use singular learning theory to study how training data shapes model behavior.
We use this understanding to develop new tools for AI safety. Read more.
By Wang and Murfet
Mechanistic interpretability aims to understand how neural networks generalize beyond their training data by reverse-engineering their internal structures.
By Gordon et al.
Spectroscopy infers the internal structure of physical systems by measuring their response to perturbations.
By Elliott et al.
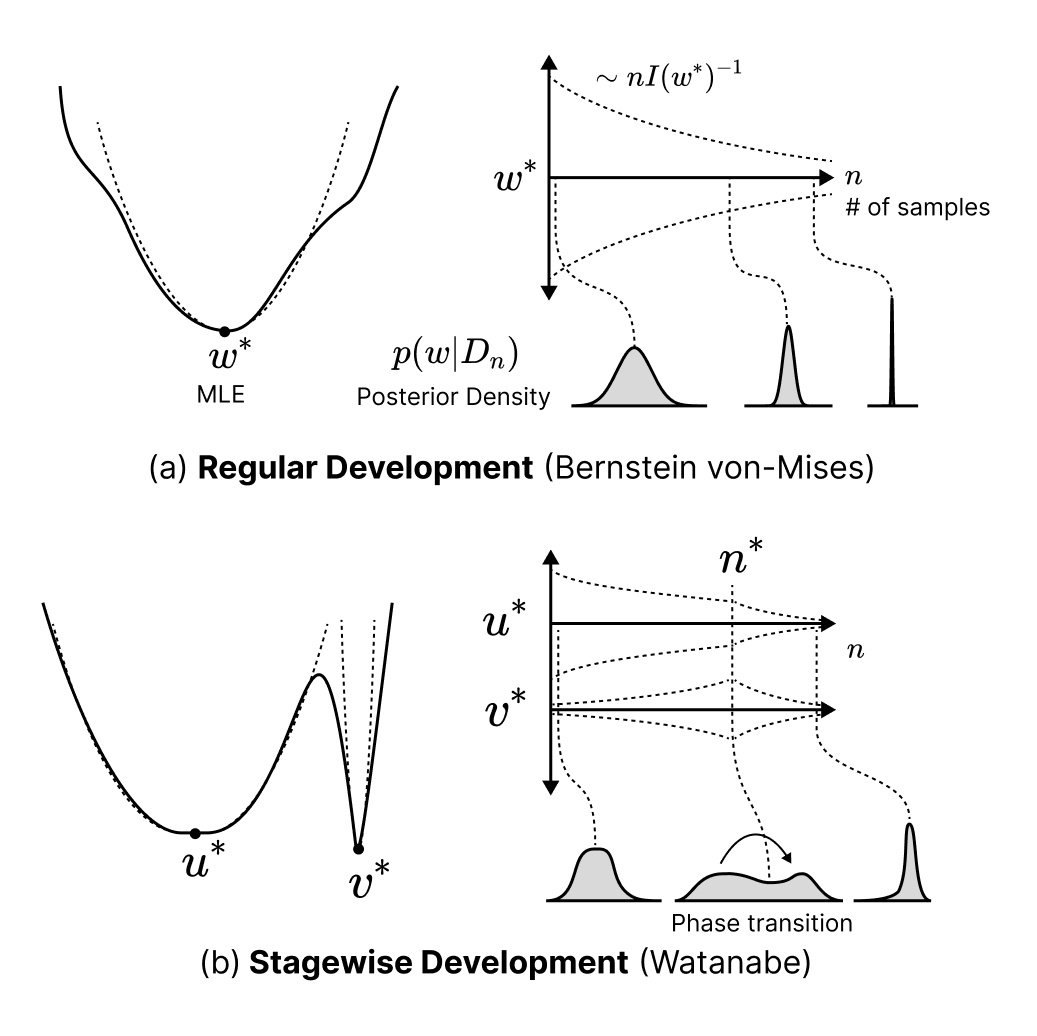
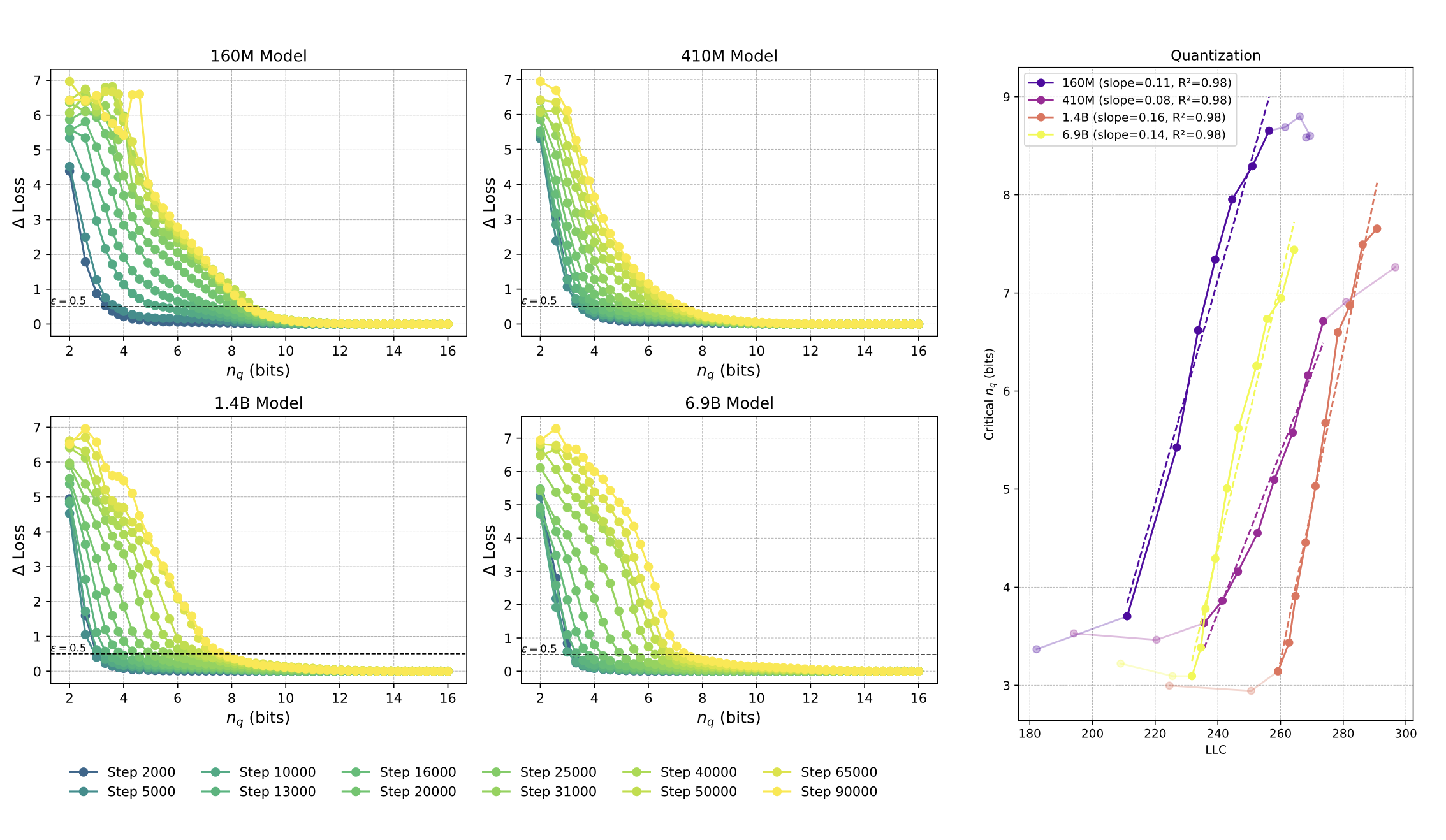
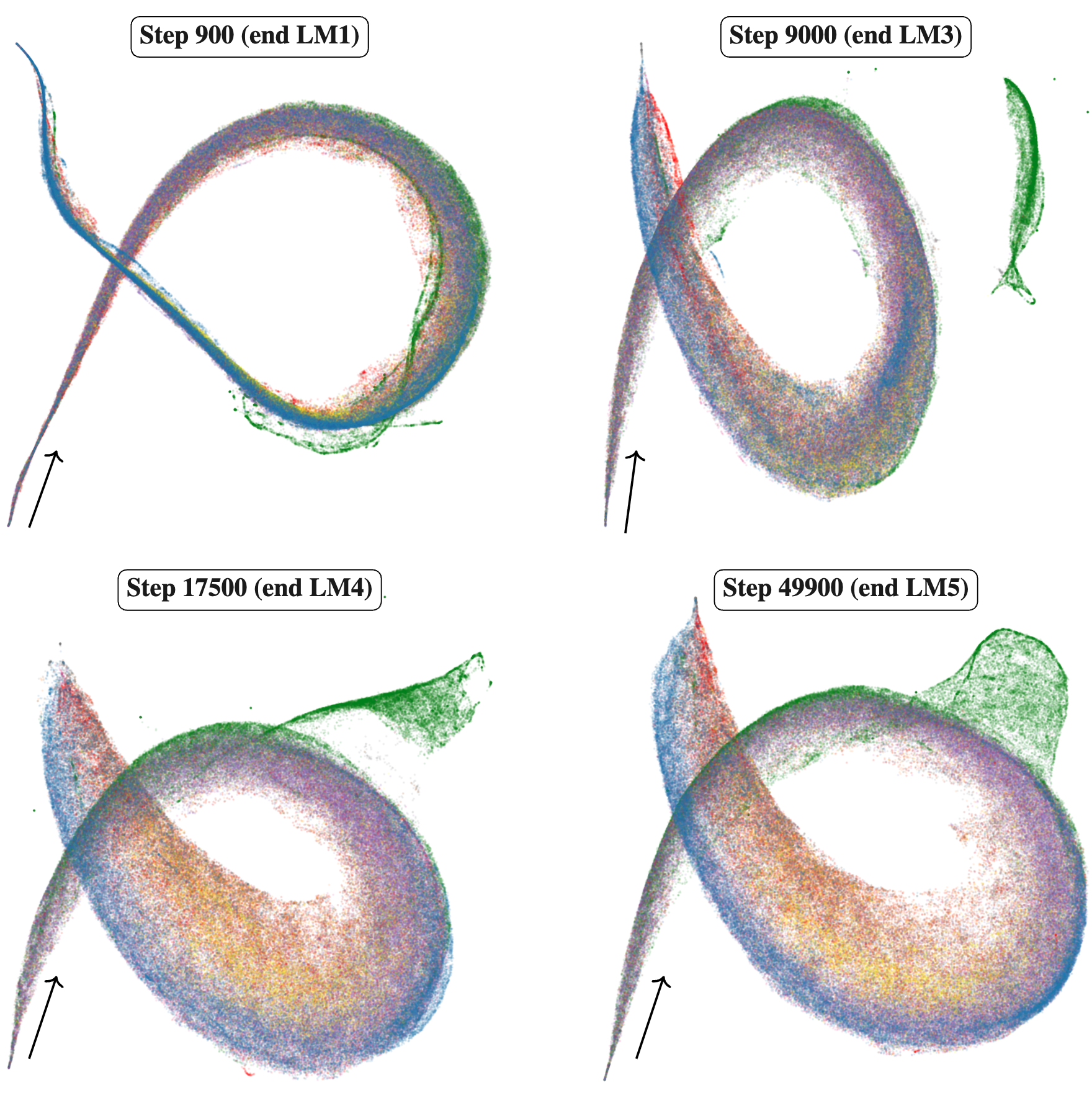
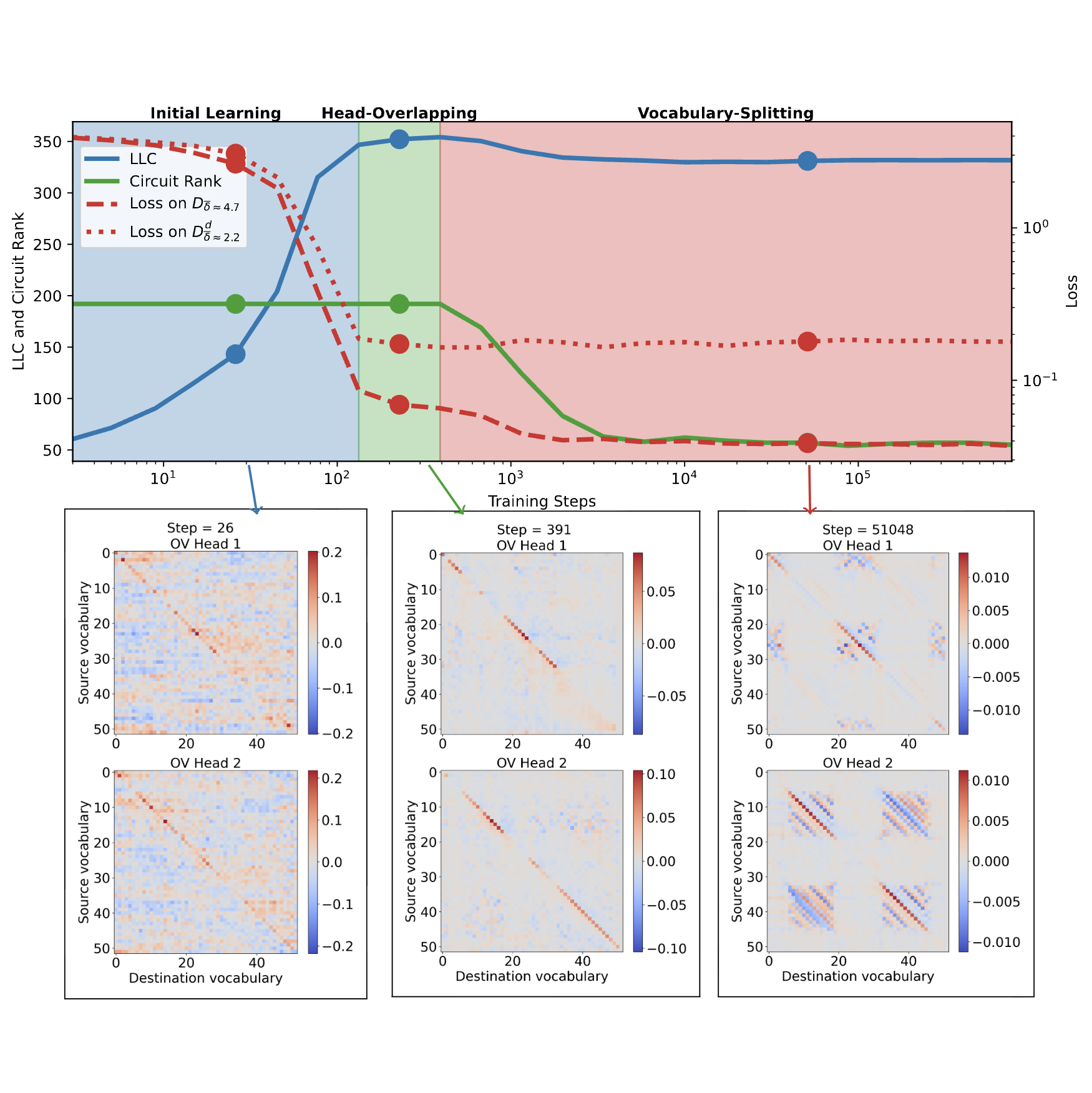
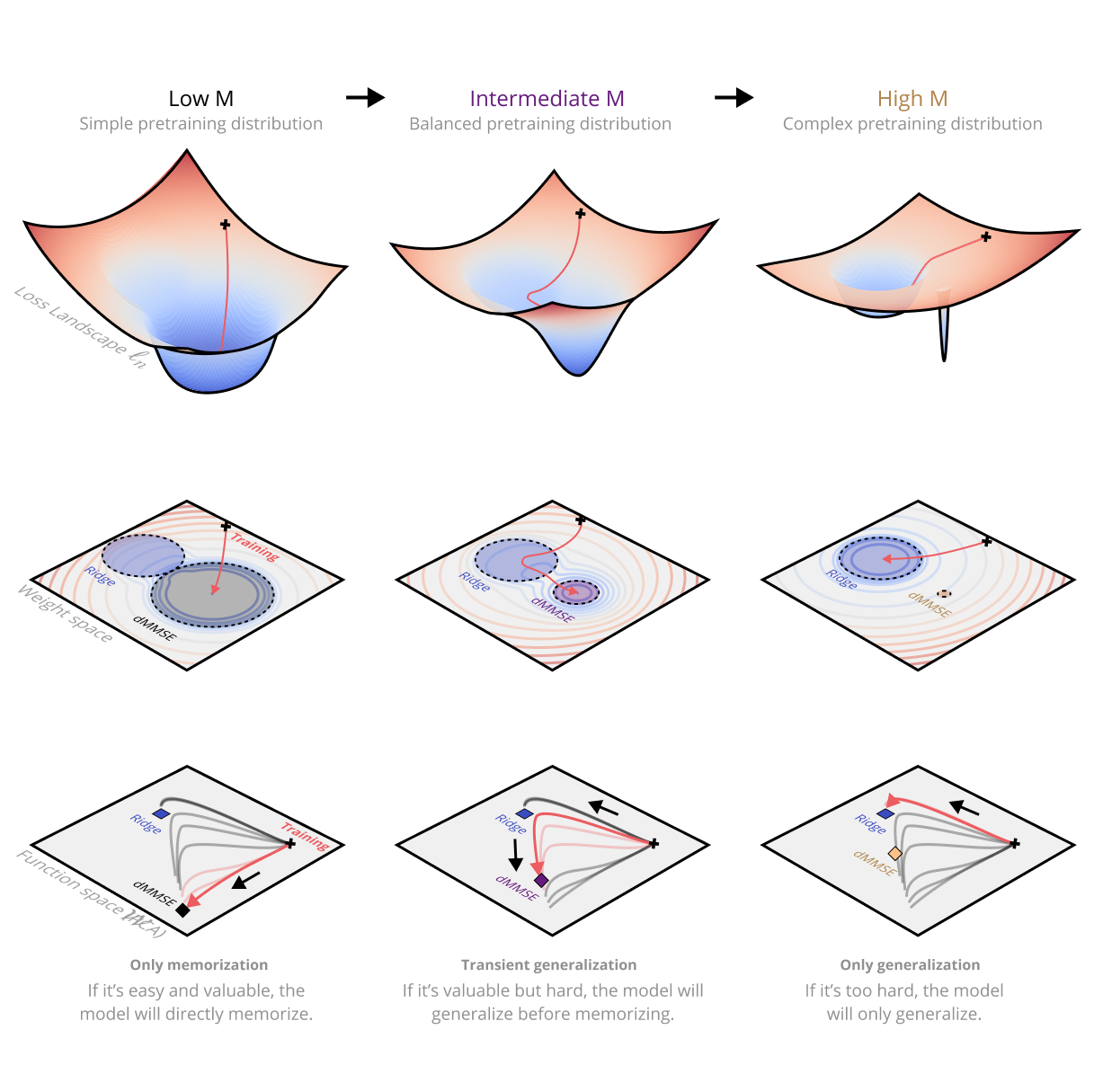
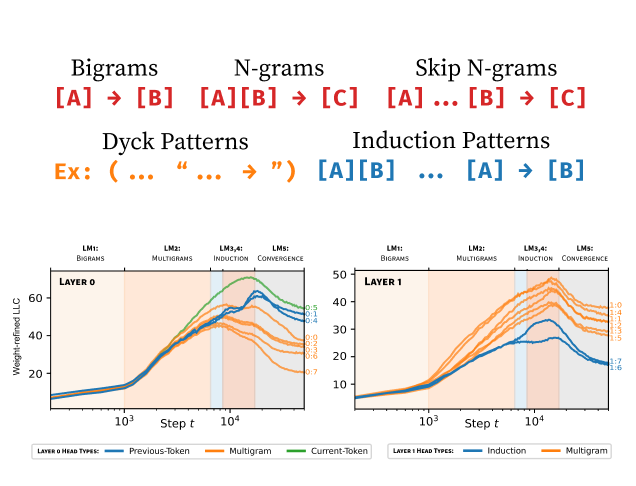
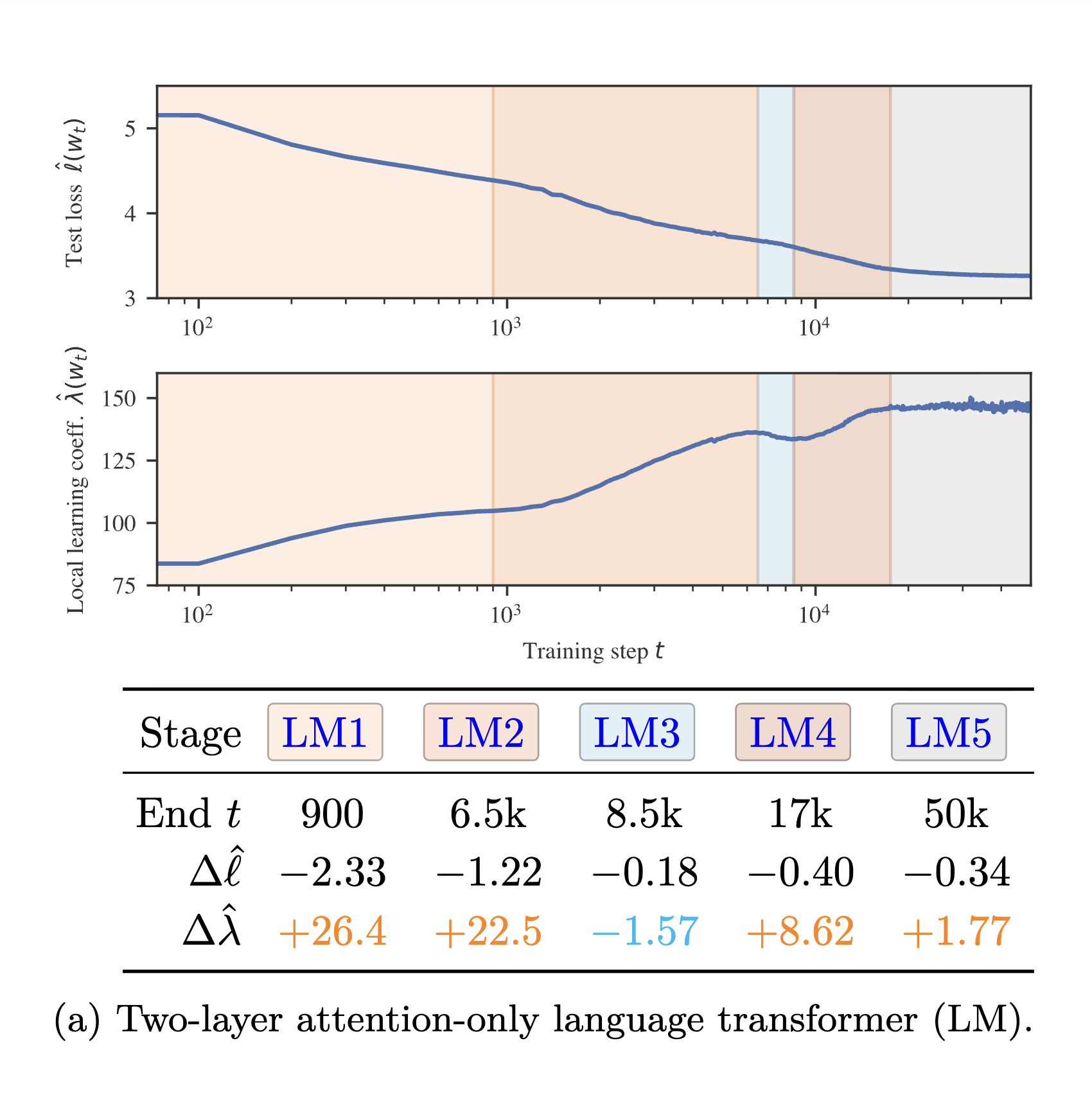
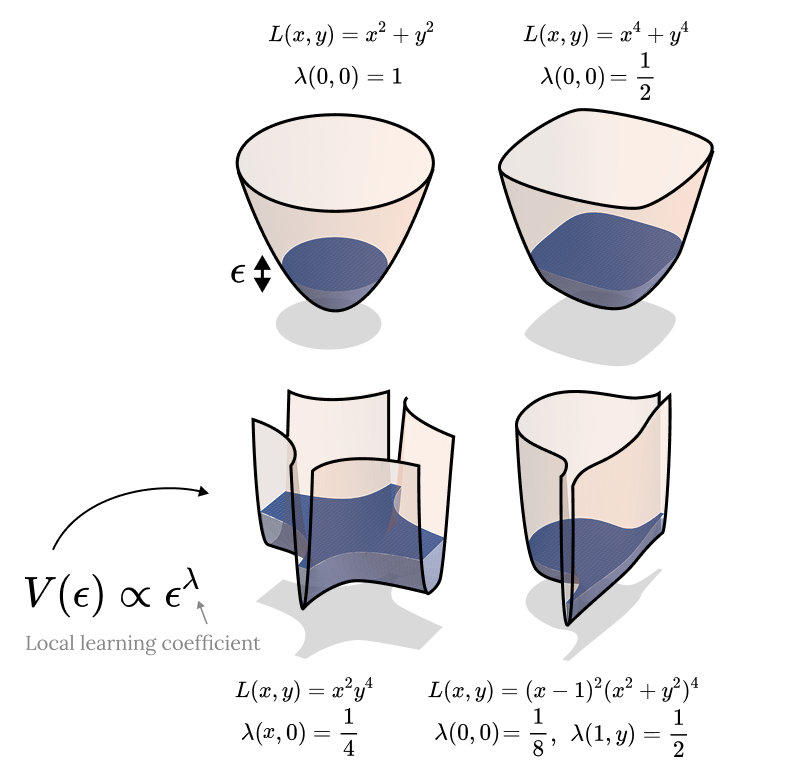
Singular learning theory characterizes Bayesian learning as an evolving tradeoff between accuracy and complexity, with transitions between qualitatively different solutions as sample size increases.
By Lee et al.
Current training data attribution (TDA) methods treat the influence one sample has on another as static, but neural networks learn in distinct stages that exhibit changing patterns of influence.
By Urdshals et al.
We study neural network compressibility by using singular learning theory to extend the minimum description length (MDL) principle to singular models like neural networks.
By Adam et al.
We introduce the loss kernel, an interpretability method for measuring similarity between data points according to a trained neural network.
By Kreer et al.
Classical influence functions face significant challenges when applied to deep neural networks, primarily due to non-invertible Hessians and high-dimensional parameter spaces.
By Wang et al.
Understanding how language models develop their internal computational structure is a central problem in the science of deep learning.
By Hitchcock and Hoogland
Degeneracy is an inherent feature of the loss landscape of neural networks, but it is not well understood how stochastic gradient MCMC (SGMCMC) algorithms interact with this degeneracy.
By Chen and Murfet
We develop a geometric account of sequence modelling that links patterns in the data to measurable properties of the loss landscape in transformer networks.
By Baker et al.
We develop a linear response framework for interpretability that treats a neural network as a Bayesian statistical mechanical system.
By Murfet and Troiani
We develop a correspondence between the structure of Turing machines and the structure of singularities of real analytic functions, based on connecting the Ehrhard-Regnier derivative from linear logic with the role of geometry in Watanabe's singular learning theory.
By Lehalleur et al.
In this position paper, we argue that understanding the relation between structure in the data distribution and structure in trained models is central to AI alignment.
By Urdshals and Urdshals
We study how a one-layer attention-only transformer develops relevant structures while learning to sort lists of numbers.
By Carroll et al.
Modern deep neural networks display striking examples of rich internal computational structure.
By Wang et al.
We introduce refined variants of the Local Learning Coefficient (LLC), a measure of model complexity grounded in singular learning theory, to study the development of internal structure in transformer language models during training.
By Hoogland et al.
We show that in-context learning emerges in transformers in discrete developmental stages, when they are trained on either language modeling or linear regression tasks.
By Lau et al.
Deep neural networks (DNN) are singular statistical models which exhibit complex degeneracies.
